Tabla de contenidos.
¿Conoces el valor didáctico de la Práctica digital? Llevar a cabo la Práctica digital con tus alumnos es de gran importancia para interiorizar de manera efectiva los conocimientos que han adquirido a lo largo de las sesiones. Una buena parte del conocimiento se construye en gran grupo en el aula a través de la conversación y el descubrimiento. Pero no nos podemos olvidar de la práctica sistemática, aquella que nos ayuda a interiorizar el conocimiento.
En Innovamat, proponemos una hora de práctica a la semana a través de la aplicación. La práctica es individual y personalizada, ya que el algoritmo se adapta a las necesidades de cada alumno. Pero ¿qué hace que tenga valor didáctico? A continuación te mostramos, con un buen puñado de ejemplos, cómo la práctica sistemática puede ser una herramienta con un valor didáctico significativo. ¡Vamos allá!
Características de la Práctica digital que aportan valor didáctico
La práctica reproductiva, cuando está en formato digital, nos permite personalizar el aprendizaje y conseguir una atención a la diversidad más precisa. La Práctica digital de Innovamat ofrece un itinerario alineado con la secuencia didáctica, cuya progresión responde a lo que hace el alumno, con correcciones en tiempo real. Estas son las características que hacen que las actividades tengan valor didáctico:
- Orientación al objetivo didáctico
- Riqueza didáctica
- Práctica de modelos y representaciones introducidos en el aula
- Actividades con más de una solución posible, o sin solución
- Conexiones entre actividades
- Resoluciones paso a paso
- Adaptación al ritmo del alumno
- Secuenciación didáctica de las actividades
- Ayudas específicas
- Diferentes conjuntos de números y rangos numéricos
A continuación recogemos varios ejemplos que sirven para ilustrar estas características, centrémonos en las actividades de práctica del Tramo 2 de 1º de ESO.
Orientación al objetivo didáctico
Cada actividad de la Práctica digital persigue el logro de un objetivo didáctico. El enunciado, las representaciones gráficas, las animaciones, las ayudas, etc., apuntan hacia la consecución del objetivo definido.
El Tramo 2 de 1º de ESO comienza con la ordenación de los números enteros y su ubicación sobre la línea numérica. Algunas de las primeras actividades son la A202, la A203 y la A204, cuyo objetivo es trabajar saltos hacia delante y hacia atrás sobre la línea numérica vacía (LNV).
- Cuando empieza, el alumno ve la representación de la LNV, donde puede dibujar los saltos que desee para responder al enunciado, que puede ser, por ejemplo:
- «Salta 12 unidades hacia delante desde el -7»
- «¿Cuál es la distancia entre los dos números?»
- «Determina el punto de origen del salto»
- Si el alumno pide ayuda, el salto se descompone en dos para facilitar el cálculo. Es una estrategia que podrá aplicar las próximas veces que realice la actividad.
En los siguientes ejemplos, se destaca la descomposición del salto pasando por el 0, una extensión del paso por el 10 especialmente útil para los enteros.

Riqueza didáctica
Práctica de modelos y representaciones introducidos en el aula
Las actividades A206, A207 y A208 permiten trabajar la representación de enteros con fichas, un modelo que previamente se ha visto en las sesiones de aula.
Por ejemplo, en la A206 se pide indicar el número entero que aparece representado gráficamente, mientras que en la A207 hay que identificar todas las representaciones equivalentes a un número dado. De esta manera, pueden consolidar la representación de enteros con este modelo.

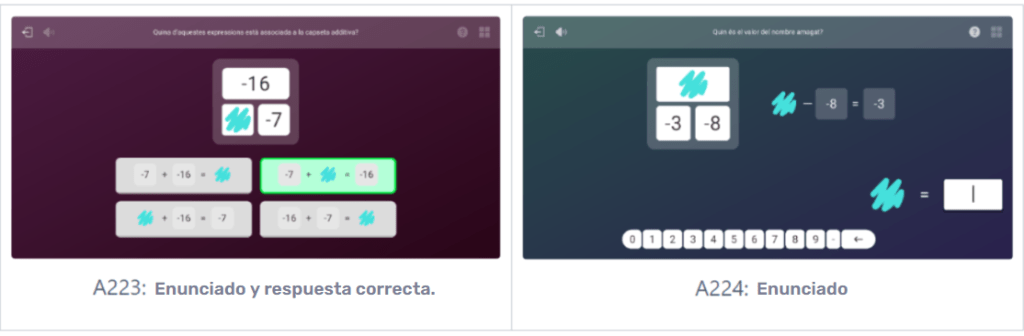
Otra representación introducida en el aula es la cajita aditiva, que permite descubrir propiedades de las operaciones aditivas y que es de gran utilidad para resolver ecuaciones con la estrategia de cover-up. Esta representación, pues, también la encontramos en la Práctica digital. Por ejemplo, en la A223 se pide identificar la expresión asociada a la cajita aditiva, y la A224 la emplea para introducir enunciados que requieren encontrar el valor de una incógnita.
Actividades con más de una solución posible, o sin solución
A veces, se plantean actividades con más de una respuesta posible, y la aplicación las acepta todas. Por ejemplo, la A217 acepta como correcta cualquier combinación de números enteros que hagan cumplir la igualdad en una operación dada. También se proponen actividades sin solución, en las que el alumno tiene la opción de responder precisamente eso.

Conexiones entre actividades
Las actividades anteriores conectan con la actividad A200, en la que se pide identificar la posición que ocupan las banderas situadas en un intervalo de la línea numérica que está dividido en partes iguales. Si el alumno pide ayuda, aparece un mensaje de texto que pregunta cuál es la distancia entre los dos números dados, una destreza trabajada en las actividades A202, A203 y A204.

Resoluciones paso a paso
Un aspecto que ayuda al alumno a detectar errores y aprender de forma autónoma es ver, al final de la actividad, la resolución paso a paso. Por ejemplo, en la A231, después de dos intentos, se muestra una animación con todo el proceso de resolución de la ecuación por cover-up, y en la A232 se muestra el árbol de resolución de la operación combinada.

Estos ejemplos muestran diferentes elementos del diseño de las actividades que permiten conseguir una práctica ajustada a la secuencia didáctica, con ayudas adecuadas al progreso de cada alumno. También son un refuerzo de lo que esperamos que registren los alumnos cuando hagan práctica sobre el papel.
Adaptación al ritmo del alumno
Secuenciación didáctica de las actividades
Como explicamos en el artículo La práctica digital con la app Innovamat, el algoritmo propone las variantes o packs de cada actividad siguiendo el orden de la secuencia didáctica, y los vuelve a recuperar a lo largo del curso para reforzar una práctica helicoidal.
Fijémonos en la práctica de multiplicaciones y divisiones de enteros, que precede a las operaciones combinadas, y que se trabaja en actividades como la A226, la A227 y la A228: primero, proponemos resolver multiplicaciones y divisiones, e indicar el resultado; después, seleccionar operaciones multiplicativas equivalentes, y, finalmente, ordenar multiplicaciones y divisiones según el resultado.
Las operaciones combinadas con enteros se practican en la A232, que incluye diferentes packs para favorecer la práctica gradual. Se empieza por enunciados con dos operaciones (por ejemplo, una suma y una multiplicación), y se acaba con combinaciones de cuatro operaciones en las que pueden aparecer potencias y paréntesis.
En los packs iniciales, se focaliza la práctica en la prioridad de las operaciones: el alumno selecciona en cada paso cuál es la operación que quiere hacer y el resultado se calcula automáticamente. En los packs más avanzados, después de la selección de la operación, el alumno debe escribir el resultado.

Ayudas específicas
Disponer de ayudas específicas en cada pack permite acompañar mejor a los alumnos según el momento en el que se encuentran. Lo vemos, por ejemplo, en la actividad A210, de sumas y restas de enteros.
En el primer pack de la A210, la ayuda permite deducir el resultado de la operación a partir del modelo de fichas, que el alumno ya domina después de haber superado las actividades precedentes: una ficha verde y una amarilla se cancelan la una con la otra, y las fichas restantes representan el resultado de la suma.
En el segundo pack de la A210, los números son mayores, y el formato gráfico de la ayuda se adapta a este cambio representando los enteros con barras horizontales.

Encontramos también una gran diversidad de ayudas en la actividad A231, cuyo objetivo es practicar y entrenar la manera de registrar la estrategia de cover-up:
- Empezamos con packs que solo piden que el alumno seleccione qué paso quiere realizar, y el paso se valida y se registra automáticamente. En caso de que pida ayuda, se le indica que pulse la última operación que resolvería en una operación combinada. Hay disponible una segunda ayuda, más gráfica, que indica la parte que hay que tapar a la hora de hacer cover-up.
- En packs más avanzados se pide y se valida tanto la operación como el resultado. También aquí hay una ayuda específica, que, además, conecta con la representación de la cajita aditiva o la multiplicativa.

Diferentes conjuntos de números y rangos numéricos
Utilizar datos de diferentes rangos numéricos es una de las maneras que empleamos para aumentar gradualmente la dificultad de la actividad y, así, adaptar la práctica al ritmo de cada alumno.
Lo hemos podido observar en el ejemplo de la A210: en el primer pack los números se encuentran en el rango [-20, 20], y en el segundo, en el rango [-100, 100]. También en la A231, que acabamos de ver, la atención a la diversidad en la práctica del cover-up se regula, en parte, con los conjuntos numéricos de cada pack. En los primeros, los números son naturales, pero, en packs más avanzados, tanto los operandos del enunciado como el resultado son enteros.

A través de los últimos ejemplos, hemos podido comprobar cuáles son las características que hacen que la Práctica digital de Innovamat tenga tanto valor didáctico. En este punto, nos podríamos preguntar sobre la vivencia real de un alumno durante una sesión de práctica digital. ¿Se concentra? ¿Está motivado? ¿Cuántas operaciones hace en 40 minutos? Encontraréis las respuestas a estas y otras preguntas en el siguiente artículo.







