Neus Sanmartík (2009) hauxe dio ebaluazioari buruz egindako lan oso gomendagarrian: lehenengo berrikusi beharreko alderdietako bat gaitasunen lorpen-maila ebaluatzeko proposatzen diren jarduerak dira. Haren hitzetan, ohiko idatzizko proben bidez ebaluatzen badugu, hau da, eginiko galderei erantzun jakinak emanez, ez da ezer aldatuko.
6 edo 7 urteko haurrekin ikasgelan nahikoa denbora lan egin duen edozein irakaslek errazago ikusiko du hori, adin horretan hizkuntza-gaitasunaren jabetze-mailak asko mugatzen baitu komunikatzeko, argudiatzeko edo ebazpen estrategia bat idatziz azaltzeko gaitasuna. Beraz, ohiko idatzizko probetatik harago, nola lor ditzakegu gaitasunetan oinarrituz ebaluatzeko ebidentziak?
Jarduera aberatsekin prozesuak ebaluatzea
Gakoa gaitasunen esparrua menderatzean datza (hau da, zer prozesu lantzen ari garen eta gure ikasleengandik zer espero dugun jakin behar dugu), eta arreta jartzean, adibidez, haien irudikapen bisual edo grafikoetan, edo gelako solasaldietan egiten dituzten esku-hartzeetan, batez ere, haurrak txikiak direnean.
Ildo beretik jarraituz, Innovamatek proposatzen dituen jarduera aberats batzuk hautatu ditugu, bereziki egokiak iruditzen zaizkigunak aipatutako baliabideen bidez ebaluatzeko. Jarduera hauek ez dira ebaluatzeko egokiak diren bakarrak, baina irakasleok egoki deritzogun beste edozein jarduera aberats ebaluatzeko aholkuak eta orientabideak ematen dituzte.
Ikus dezagun adibide konkretu baten bidez: neurriari buruzko jarduera bat egin zuten LHko 1. mailako ikasle batzuen benetako kasua. Jardueran, ikasleek koadernoan zituzten objektu batzuk neurtu behar zituzten hiru luzera-neurri desberdin erabiliz (hatzak, kubotxoak eta haien aukerako beste bat).

Zer ebalua dezakegu era honetako jarduera batean? Hasteko, 1etik 20ra arteko ondoriozko zenbaketa eta zenbaki horien idazketa. Eduki horiek ezinbestekoak dira; izan ere, ez badira ongi menderatzen, jarduera osoa baldintzatuta geratzen da.

Kasu honetan, erantzun batzuetan zenbakiak handiegiak direla ikusten dugu, hala nola “30 arkatz” edo “54 hatz”. Ziur aski, ikasle honek zenbakiekin ditu zailtasunak, eta ez neurriarekin.
Zenbaki horiek nola irakurtzen diren galde diezaiokegu, eta beste zenbaki bat erreferentziatzat hartuta, hark idatzitakoak handiagoak ala txikiagoak diren galdetu.
Gainera, agerikoa da ikasleek neurriaren inguruko ezagutza jakin batzuk erabili beharko dituztela. Adibidez:
- Neurketa-teknika zehatza erabiltzen al du hatzekin neurtzerakoan?

Kasu honetan, ikasleak bi eskuetako hatz erakusleak kateatu ditu objektuarekiko perpendikularki ipiniz; horri esker, kontsistentea da eta beti neurri bera lortzen du.

Aldiz, ikasleak hemen hatz erakusle bakarra erabili du objektuaren gainean “saltoka” mugitzeko. Era horretara egitean, noraino neurtu duen adierazten duen puntu zehatza galdu du behin eta berriz, eta hatza berriz irudiaren gainean jartzean, neurtu gabeko tarteak utzi ditu, edo dagoeneko neurtutako tarte bat berriz neurtu du.
Esango diogu teknika hau ez dela zehatza, eta, horrela eginez gero, neurtzen duen bakoitzean erantzun desberdin bat lor dezakeela, nahiz eta beti hatz eta teknika bera erabili.
Zera galde diezaiokegu: «Nola egon zaitezke ziur hatza altxatu eta berriro irudiaren gainean jartzerakoan ez zarela lehengo leku berean jartzen ari?».
Jarrai dezagun. Jarduera honetako zereginen artetik, gaitasunetan gehien oinarritzen dena neurketa-unitate bat zentzuz aukeratzeko zeregina da. Geure buruari zera galde diezaiokegu:
- Ikasleak ziurtatzen al du neurketa-unitate gisa beti luzera bera duen objektu bat aukeratzen duela?

Hemen, ikasleak borragoma bat erabili du orientazioa aldatu gabe.

Hemen, aldiz, plastifikatutako zenbakien txartelak erabiliz egin du neurketa. Batzuetan, plastifikatutako marjina eta guzti neurtu du, eta, besteetan, txartelaren zati zuria kontuan izanda bakarrik neurtu du, marjina alde batera utzita.
Ikasleak egindakoak ez duela koherentziarik ikus dezan, berriro objektu bera neurtzeko eskatuko diogu, eta ea emaitza bera lortu duen galdetu.
Bestalde, jarduera honek prozesu matematikoen ohiko gaitasun batzuk barne hartzen ditu. Problemak ebaztea prozesuari dagokionez, zera plantea genezake:
- Ikasleari neurketa-unitate bat aukeratzeko eskatu diogunean, aukerarik onena hautatu al du?
Kasu horretan, interesgarria da nabarmentzea “onena” kontzeptua ikaslearen irizpideen arabera zehaztu daitekeela. Zer zen ikaslearen helburua: zehatza izatea, ala eraginkorra izatea? Edo biak?
Ikus ditzagun beste adibide batzuk:

Ikasle honek borragoma bat erabiltzea aukeratu du. Modu horretan, zehatza izan da (elementuari soilik erreferentzia eginez eta ez teknikari, horrek zehaztasun-mailari ere eragingo baitio), neurketa-unitatea hainbat aldiz sartzen baita neurtutako objektuaren luzeran. Gainera, bere koadernoan «4 eta erdi» erregistratu du.

Beste ikasle honek, berriz, arkatz bat erabiltzea erabaki du, eta horri esker eraginkorragoa izan da, behin bakarrik neurtu behar izan baitu erantzuna lortzeko.
Bi kasuetan komeni da galdetzea bai zein irizpide erabili duten, bai beste irizpide bat kontuan izanda nola egingo luketen.
Hori ere Problemak ebaztea prozesuari lotuta dago. Geure buruari galdera hau egin diezaiokegu:
- Egiaztatzen al du lortu duen erantzuna zentzuzkoa dela?

Hartutako neurrien zehaztasuna baloratu gabe, ikusiko dugu erantzunek zentzua dutela haien arteko loturari dagokionez.
Hatzak eta kubotxoak erabiliz adierazitako erantzunak bat datoz begi hutsez ikusten denarekin: sugandila dela elementurik luzeena, eta ehunzangoa laburrena.
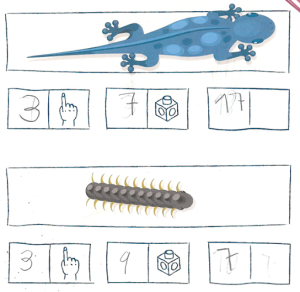
Kasu honetan, ez da zentzuzkoa begi hutsez argi eta garbi luzera desberdina duten bi marrazkik neurri bera edukitzea (3 hatz). Erantzunak logika gutxiago du kubotxoekin neurtutako luzerak desberdinak direla ikustean.
Interesgarria litzateke haurrari hori agerian uztea galderak eginez, eta gidatu egingo dugu emaitzak berrikustearen garrantzia plantea dezan.
Azkenik, galdera batzuk egin genitzake Arrazoiketa eta proba prozesuari dagokionez lortu duen jabetze-maila neurtzeko:
- Gai al da justifikatzeko zergatik neurtzen duen modu jakin batean?

Ikasle honek, hatzekin neurtzeko, 5 hatzak erabili ditu aldi berean. Zergatik egin duen horrela galde diezaiokegu.
Gerta liteke ikasleak hori justifikatzen ez jakitea, ala, aitzitik, esatea horrela azkarrago neurtuko duela.
Eta Arrazoiketa eta proba prozesuari buruzko azken galdera:
- Ikasleak ikusten al du kubotxoekin neurtzea fidagarriagoa dela hatzekin neurtzea baino?
Hasieran genioen moduan, 6 edo 7 urteko ikasle bati idatziz arrazoitzeko eskatzea ez da agian prozesuak ebaluatzeko modurik egokiena. Beraz, kontuan izan behar dugu ikasgelan sortzen diren elkarrizketak ere ebaluatzeko aukera:
Ikasgelan elkarrizketaren bidez lor dezakegun beste alderdi positibo bat zera da: ikasle batek ez badu galdera bat zehatz erantzuten, irakasleak elkarrizketa unean bertan kudea dezake ikaslea benetan zer ari den arrazoitzen jakiteko.
Ebaluazioa Innovamaten
Innovamaten ebaluazioaren funtzio nagusia alderdi formatiboa dela defendatzen dugu; hau da, ebaluazioak ikasleei beren ikaskuntza-prozesua erregulatzeko aukera eman behar dio. Zentzu horretan, gure ikasleei nabarmen lagunduko diena artikulu honetan zehar egin ditugun iruzkinak haiekin partekatzea da. Hori eginez gero, ikasleak ebaluatzen ariko gara, eta ez kalifikatzen.
Aldi berean, zeregin hau ikaskuntza-prozesuaren emaitzak kalifikatzeko (notak jartzeko) erabili nahi badugu, ebaluazio-adierazle gisa zerrendatu ditugun galdera desberdinak erabil genitzake eta, egoki irizten badiogu, ponderazioa egin.
Ikusi dugunez, uneoro zer beha dezakegun jakiteak eta ikasleen benetako erantzunen adibide batzuk eskura izateak asko lagunduko digu ebaluatzeko lan zailean.
- NCTM (2000): Principles and Standards for School Mathematics. Reston, VA, Ameriketako Estatu Batuak
- Sanmartí, N. (2020) Avaluar és aprendre: L’avaluació per millorar els aprenentatges de l’alumnat en el marc del currículum per competències. Direcció General de Currículum i Personalització. Departament d’Educació. Bartzelona, Espainia






