Zure matematika - ikasgela eraldatzeko tresna
Argi dago ez geniokeela biderketarik egiteko eskatuko oraindik batzen ez dakien ikasle bati. Gaia hurbilagotik aztertzean, konturatuko gara biderkatzea zenbaki berbera behin eta berriz batzea dela; beraz, ondo ulertu behar da hasieratik zer den batuketa bat egitea. Izan ere, matematiken ikaskuntzak, batez ere zenbakizko zentzuaren barruan, izaera sekuentziatua du: kontzeptu berri bat ulertzeko, aldez aurretik egindako lanean oinarritu behar dugu, eraikuntza batean adreiluak bata bestearen gainean jartzen ditugun bezala.
Matematika-ikaskuntzako ibilbideak
Hori dela eta, suma dezakegu ezagutzen ditugun kontzeptu eta trebetasun matematikoen aterkipeaneskeleto bat dagoela, egitura bat, ikasle batek ikas ditzakeen trebetasunak sekuentziatzen dituena. Hortik dator ikaskuntza-ibilbideen kontzeptua. Azken 25 urteetan didaktikan espezializatutako artikulu eta aldizkarietan itxura hartzen joan den kontzeptua da, eta eraldatzeko ahalmena duela erakutsi du. Izan ere, ikaskuntza-ibilbideak definitzeak hezkuntzako bi eragile nagusiei eragiten die: ikasleei eta irakasleei. Irakasleoi trebetasun matematiko baten bilakaera ezagutzeak aukera ematen digu jakiteko ikasle batek zer urrats eman dituen dagoen tokira iristeko, eta, aldi berean, hortik aurrera ikas lezakeenaz jabetzen laguntzen digu. Horrela, erabaki didaktiko egokiagoak eta dokumentatuagoak har ditzakegu. Ibilbide horiekin batera ikaskuntza-etapa bakoitzari lotutako zeregin espezifikoak egiten baditugu, ebaluazio formatiboa egiteko tresna bikaina izango dugu esku artean (Morales eta Fernandez, 2022). Izan ere, hainbat ikerketaren arabera, ikaskuntza-ibilbideak oso eraginkorrak dira irakasleentzako prestakuntza-tresna gisa (Wilson, 2013; Sarama, 2017), ikasleen matematika-ikaskuntza hobetzeko tresna gisa (Clements, 2011) eta baita ikerketan oinarritutako irakaskuntzarako marko teoriko baten oinarri gisa ere (Sztajn, 2012).
Innovamaten sekuentzia didaktikoa
Oro har, ikaskuntza-ibilbideak trebetasun jakin batzuentzat eraiki dira, hala nola, zenbaketarako edo neurriaren zentzua eraikitzeko. Duela gutxi egindako ikerketa batzuek ibilbide horiek garatzeko ahaleginak egin dituzte. Horren harira, Innovamaten galdera bat sortu zitzaigun, ia premia bat: posible ote zen sekuentzia txiki horiek guztiak matematikaren ikaskuntzan interdependentzia guztiak irudikatzen zituen mapa batean elkartzea? Eta, erronkak gustatzen zaizkigunez, horretan hasi ginen.Ikertzen, irakurtzen eta adituekin hitz egiten urtebete baino gehiago egon ondoren, eta ideiak eztabaidatu eta adosteko hainbat bileraren ostean, prest dugu 3 eta 12 urte bitarteko ikasleek klasean lantzen dituzten eduki matematikoen maparen lehen bertsioa! Oraindik mapa garatzen jarraitzen dugu, ikasleek beste adin batzuetan landu ohi dituzten edukiekin. Horrelako lan bat egiteko erabaki konplexu asko hartu behar izan ditugu, eta lana bizirik mantenduko dugu beti, etengabe joango baikara informazioa gehitzen eta hobetzen. Atal asko egiteko bibliografia espezializatua erabili dugu, baina ziur gaude aurkikuntza berriak egongo direla, eta aurkikuntza horiek mapa zehazten eta hobetzen lagunduko digutela.
Berezitasun batzuk azalduko dizkizugu mapa nola eraikita dagoen ulertzeko eta behar bezala interpretatu ahal izateko.
“Mapa”, izatez, grafo bat da: multzo bakoitza ikasketa-unitate txikiz osatuta dago (nodo deitzen zaie), eta edukiak geziz elkarlotuta daude, “A → B” gezi batek honako hau adierazten du: ikasle batek ez badu lortzen A-k proposatzen duena egitea, ziur aski ez du lortuko B-k proposatzen duena egitea ere. Garrantzitsua da azpimarratzea, hala ere, gezi horrek ez duela esan nahi A-ren hurrengo urratsa B denik. Izan ere, nodo gehienetatik gezi bat baino gehiago sartu eta ateratzen dira. Zenbakizko zentzuari dagokion grafoaren atalak, adibidez, itxura hau du urrutitik begiratuz gero:
Itogarria, ezta? Oraintxe bertan 2000 nodo eta milaka gezi inguru daude. Helburua, beraz, ez da ikaskuntza-mendekotasunak hain modu orokorrean irudikatzea, baizik eta kontzeptuak elkarlotuta dituen sare handi hau erabiltzea, ikasgelan ezagutza eraikitzen lagunduko diguten tresnak sortzeko.
Proiektuaren hasierako motibazioetako bati helduz (gerora, aurreikusi ez genituen beste arlo batzuk aldatu dira), ibilbide bakarra izateak ikasle batek ikasten jarraitzeko behar dituen laguntzak bideratzeko aukera ematen digu. Demagun Larraitzek zailtasunak dituela algoritmo bertikalarekin batuketak egiteko. Grafoa aurrean izanda, era honetako galderak egingo dizkiogu gure buruari: ikaslea gai al da bi batugaiko batuketa bat ebazteko, non bi batugaien batekoek ez duten hamarrekorik batzen? Ez bada gai, jakingo al luke batuketa berbera manipulazio bidez ebazten, 10 oinarriko blokeak erabiliz? Bestela, ba al daki Larraitzek zenbaki bat irudikatzen 10 oinarriko materiala erabiliz? Edo, gai al da dagokion tartean banaka eta hamarnaka zenbatzeko? Prozesu horri jarraituz, atzeraka joan gaitezke grafoan Larraitzen zailtasunaren jatorria non dagoen detektatu arte, eta ikasketa-puntu horri lotutako baliabideak erabil ditzakegu, konponbidea bilatzen lagunduko diguten zereginak edo gidak bilatzeko. Mapari esker, edozein edukirekin egin dezakegu hori, edukia edozein bloketakoa izanda ere.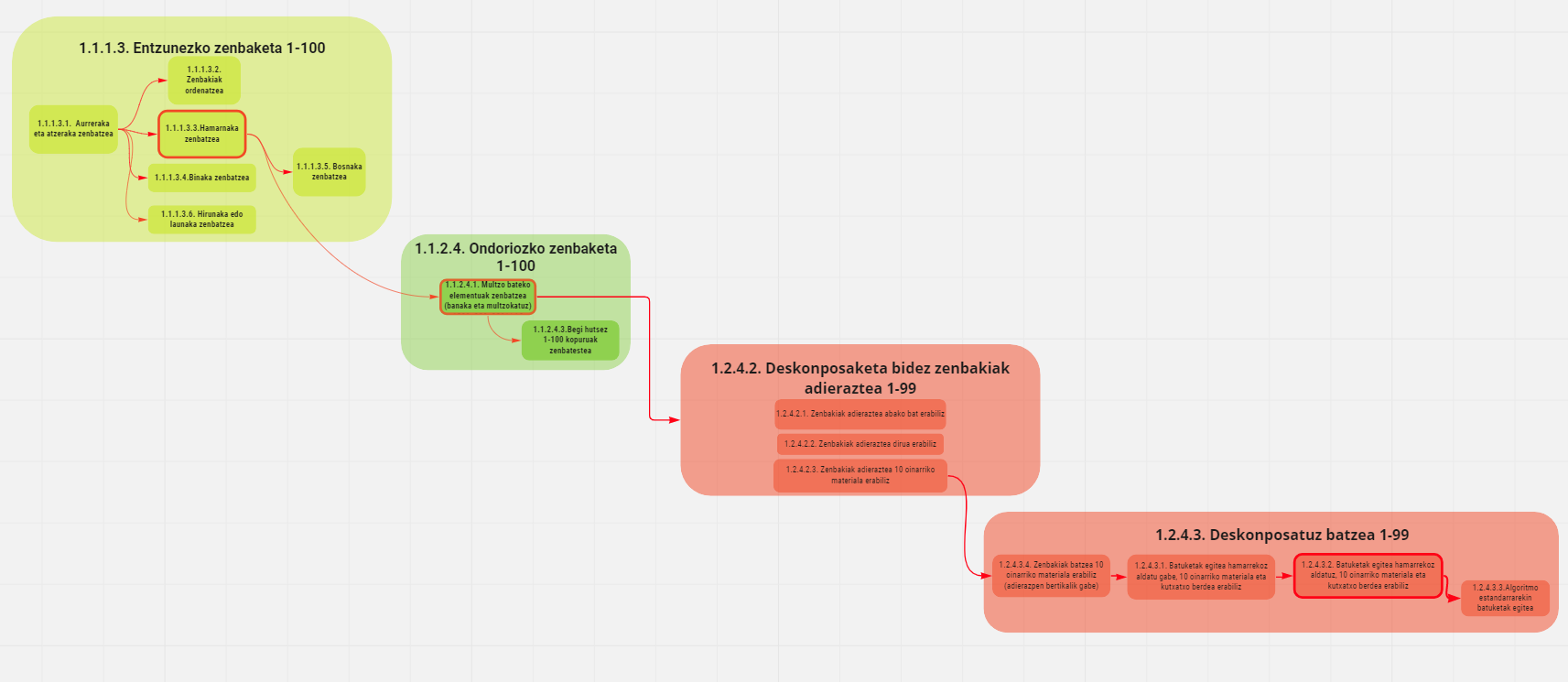
Edukiak eta prozesuak
Gaitasun edo konpetentzia matematikoaren inguruan dugun ikuskera dela eta, garrantzitsua da azpimarratzea grafoan edukiak soilik agertzen direla: ez die erreferentziarik egiten jarduera matematikoen azpiko prozesuei (problemak ebaztea, arrazoiketa eta proba, loturak, komunikatzea eta adieraztea). Hala ere, edukiak aipatutako prozesuak garatzeko egokiak ez diren irakaskuntza-jarduerekin edo -jarrerekin lantzen badira, mapa honen eta antzeko tresnen potentziala oso mugatuta geratuko da. Ez dugu nahi irakaskuntza nodo hauen arteko ibilbide soila izatea; aitzitik, grafoak zeharkako ikuspegia ematea nahi dugu, edukiak zer ordenatan eraikitzea komeni den jakin dezazuen.
Beste puntu interesgarri bat da, era berean, halako egitura bat erraz programa daitekeela makina batek irakur dezan. Horrek aukera ematen digu tresna digitalen bidez ikaskuntza indibidualizatzeko. Izan ere, Innovamateko ikasleek, astero, ikasgelan ikusitako edukiak sistematikoki praktikan jartzen dituzte App-a erabiliz. Hortik ateratzen diren datuak, maparen bidez ondo interpretatuz gero, oso baliagarriak dira ikasle bakoitza zein etapatan dagoen, eta zer indartu, praktikatu edo esploratu dezakeen identifikatzeko. Informazio hori ezagutzea, bakoitzak egoki iritzitako xehetasun-mailan, oso baliotsua da irakasleok gure ikasleen ikaskuntza-prozesuari buruzko ikuspegi zabalagoa izan dezagun, baita hurrengo erronketan ikasleak errazago orientatzeko aukera izan dezagun ere.
Hainbeste orduz puntu eta geziekin aurrera eta atzera ibili ondoren, kontuz ibili behar dugu mapa honek eskaintzen dituen aukerekin urrunegi joan gabe. Aurkezpen labur hau egin ondoren, oraingoz bakoitzak pentsatu behar du era horretako tresna batek nola eralda dezakeen bere ikasgela eta nola orientatu ikasleak. Irakasleok duzuen denboraren eta ibilbideen inguruko interesaren arabera, agian komenigarria izan liteke mapa beste formatu batean egitea, kontsultatzeko eta kontsumitzeko errazagoa izan dadin, eta hezkuntza-komunitateko edonork eskura izan dezan. Azkenean, ikasgelari buruzko hausnarketa hori da beti eraldaketarik indartsuena.
- Douglas H. Clements & Julie Sarama (2004) Learning Trajectories in Mathematics Education, Mathematical Thinking and Learning, 6:2, 81-89, DOI: 10.1207/ s15327833mtl0602_1
- Morales, M. M. & Fernández, J. F. G. 2022, La evaluación formativa: Estrategias eficaces para regular el aprendizaje (Biblioteca Innovación Educativa no 48). Ediciones SM España.
- Wilson, P.H., Mojica, G.F., & Confrey, J. 2013 Learning Trajectories in Teacher Education: Supporting Teachers’ Understandings of Students’ Mathematical Thinking. The Journal of Mathematical Behavior, 32, 103-121.
- Sarama, J., Clements, D.H., & Spitler, M.E. (2017). Evidence of Teacher Change after Participating in TRIAD’ s Learning Trajectories-based Professional Development and after Implementing Learning Trajectory-based Mathematics Instruction. Mathematics Teacher Education and Development, 19, 58-75.
- Douglas H. Clements, Julie Sarama, Mary Elaine Spitler, Alissa A. Lange, & Christopher B. Wolfe. (2011). Mathematics Learned by Young Children in an Intervention Based on Learning Trajectories: Large-Scale Cluster Randomized Trial-era. Journal for Research in Mathematics Education, 42(2), 127–166. https://doi.org/10.5951/jresematheduc.42.2.0127
- Sztajn, P., Confrey, J., Wilson, P.H., & Edgington, C.P. 2012 Learning Trajectory Based Instruction. Educational Researcher, 41, 147 – 156.
- Siemon, D., Barkatsas, T. & Seah, R. (2019). Researching and Using Progressions (Trajectories) in Mathematics Education (Global Education in the 21st Century, 3). Brill | Sense.






