Te mostramos algunos problemas de PISA 2022
En el presente año, se han dado a conocer algunos problemas de las pruebas PISA 2022 que resultan interesantes de analizar. Mi recomendación es que los intentéis hacer antes de leer la resolución, para poder poneros en situación. Es relevante destacar que los estudiantes de 15 y 16 años, encargados de enfrentarse a estos problemas, deben lidiar con la presión de realizar un examen, representar a su país, lo cual añade un componente adicional a la dificultad de las pruebas.
Una opción que os propongo, similar a la práctica común en la formación de profesores, es intentar simular condiciones similares a las que se enfrentan los alumnos, donde se busca empatizar con los estudiantes. Por eso, he querido dejar los enunciados también en inglés, para que nos podamos poner un poco más en situación de cómo se puede sentir un alumno de 15 años en situación de examen, leyendo estos enunciados.
Por ejemplo, en la facultad de educación, presentamos la importancia del pensamiento multiplicativo, y cómo podemos construir las tablas de multiplicar, para que vean que no se deben aprender memorizando, sino que debemos llegar a su memorización entendiendo cada resultado. A los adultos en formación les hacemos aprender la tabla del 17 como se puede ver en este vídeo, que es como se puede sentir un niño de 8 años aprendiendo la del 7.
Vamos con el primer problema:
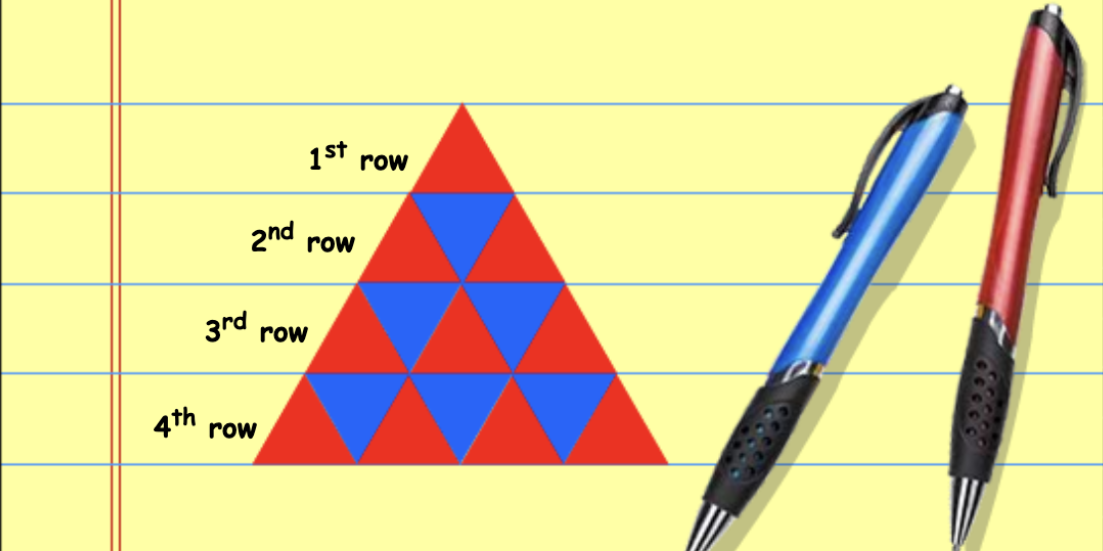
El Patrón de Triángulos


Si ya lo habéis pensado, ¡podéis seguir leyendo!
Este problema involucra la habilidad de identificar patrones. Se presenta una serie de filas con triángulos equiláteros rojos y azules, y se solicita determinar el porcentaje de triángulos azules. La resolución típica podría ser aplicar proporciones: como nos preguntan qué tanto por ciento de triángulos azules hay, muchos alumnos, o muchos de nosotros hubiéramos contado cuántos azules hay (10), de los 25 que hay en total. Y entonces hubiésemos aplicado proporcionalidad (algunos dirían regla de tres) para decir que si de 25, 10 eran azules, de 100, habría 40 azules y, por lo tanto, un 40%. Esta resolución sería típica de una aplicación de un procedimiento algorítmico. No es mucho tiempo realizar estos cálculos, que son números sencillos, pero en una prueba de más problemas quizá no nos lo podemos permitir.
Una aproximación más matemáticamente competente implica conectar el problema con la medida de áreas y comprender las proporciones entre los triángulos rojos y azules en cada fila. Darse cuenta, por ejemplo, que en cada fila siempre hay menos triángulos azules que rojos, aunque en diferente proporción: (0%, 33,3%, 40%, 42%, 44%) por lo que en total, seguro que el % de azules es menor que 50%, así, de entre las soluciones que nos proponen, sin hacer ningún cálculo, ya sabemos que será 40%.
Es fundamental cultivar la visualización de patrones y el entendimiento de las proporciones desde etapas tempranas. Este tipo de problemas requiere no solo habilidades numéricas, sino también la capacidad de hacer conexiones entre conceptos matemáticos.
Es relevante destacar que el 64% de los estudiantes a nivel mundial respondieron correctamente. Al analizar las posibles respuestas, la del 50% es la que sería más grave, ya que querría decir que ha visualizado el mismo número de azules que de rojos. Pero la del 60% es que está contestando el % de rojos, cosa que puede haber sido una equivocación, no significa que no sepas matemáticas. Y la del 66,7% es que has hecho la proporción de azul sobre rojo, no sobre el total, que también puede ser una equivocación.
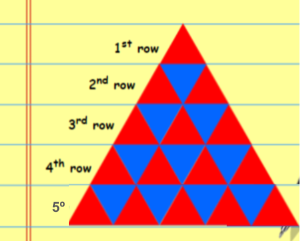
Pero, ¡cuidado! Esto solo acaba de empezar. De hecho, este problema forma parte de una serie de tres problemas. El que hemos analizado a fondo es el 2º de la serie:

Podéis encontrar esta tabla en el siguiente enlace (página 4). Así, en realidad os proponemos que entréis al entorno que entraron los alumnos cuando realizaron la prueba PISA (2022) y probéis de hacer el problema completo. Versión ESP / Versión ENG.
Pregunta 1 de 3:

Pregunta 2 de 3:

Pregunta 3 de 3:

Si nos fijamos, en la pregunta 1 de 3, solo nos hacen calcular un porcentaje, pregunta totalmente procedimental donde demuestras si sabes calcular (¿Y os habéis fijado que teníais a mano una calculadora?). En la pregunta 2 de 3, primero tienes que saber seguir el patrón, contenido específico de pre álgebra, y entonces, calcular también el porcentaje, estas dos preguntas las consideran de nivel 1 y 2 respectivamente. Pero fijaos en la pregunta 3 de 3. Lo que ya nos hacen es generalizar y aplicar el razonamiento que habíamos hecho antes, que mucha gente hubiera pensado, que para qué liarse tanto, si “aplicando una regla de tres, ya podíamos contestar”. Pues justamente consideran de nivel 5 saber generalizar y darse cuenta de que siempre va a haber menos triángulos azules que rojos en cada fila.
Y aún no hemos terminado, analizando bien la corrección, si os fijáis, en la pregunta 3 hay una parte de respuesta abierta donde valoran el razonamiento, un proceso matemático fundamental. Así, los alumnos que ven la generalización, pero su razonamiento no es del todo correcto, les puntúan con un nivel 4 en lugar de 5. Y si no lo consideran ni parcialmente correcto, no les puntúan nada y se quedan en nivel 2.
Ahora os voy a confesar que yo, aunque he escrito el argumento correcto antes cuando solo estaba contestando la pregunta 2, cuando he entrado en la web y he introducido en inglés el argumento, he puesto: “Because there will be always less blue triangles than red ones”, y aunque sabía la respuesta correcta, que arriba os he justificado mejor, me hubiesen puesto solo en nivel 4 (partial credit), porque no he escrito que eso pasa en cada fila.

En la página 247 del Informe PISA 2022 tenéis las correcciones en castellano.
El nivel de desafío y la enseñanza competencial
La resolución efectiva de estos problemas no solo se trata de conocimientos matemáticos, sino también de habilidades argumentativas y de generalización. En el contexto español, el nivel de contenido matemático requerido para abordar este problema corresponde a 6º de primaria o 1º de ESO. Sin embargo, alcanzar el nivel 5, que implica razonamiento y generalización, es posible solo a través de un enfoque educativo que fomente la comprensión profunda de los conceptos y la diversidad de soluciones, así como el trabajo profundo de los procesos matemáticos.
En este gráfico podemos ver que la gran mayoría de los jóvenes de 15 años que participaron en el estudio en nuestro país está en nivel 1, 2 y 3. Los países que mejores puntuaciones han sacado, podríamos decir que tienen a la mayoría de los participantes en los niveles 2, 3 y 4. No se observan aún países centrados en niveles 5 y 6, que supongo que es a lo que queremos aspirar, mundialmente, a largo plazo.

La gráfica completa la puedes encontrar en el siguiente enlace (página 42), que muestra el porcentaje de alumnado por niveles de rendimiento en las comunidades y ciudades autónomas españolas en PISA 2022, en orden decreciente de porcentaje de alumnado en los niveles 5 y 6.
En última instancia, el desafío de las pruebas PISA no solo radica en la capacidad de resolver problemas matemáticos, sino en la capacidad de pensar críticamente y aplicar el conocimiento en situaciones novedosas, una habilidad esencial para el éxito académico y profesional.