Un exemple d'una tasca rica de 1r d'ESO
Què necessitem per avaluar l’assoliment de continguts i processos matemàtics per part de l’alumnat? Doncs, encara que sembli una obvietat, és fonamental comptar amb una activitat que ho permeti. Si per resoldre-la només cal que l’alumne hagi memoritzat un fet concret o hagi automatitzat un procediment determinat, aquesta activitat no serà la més adequada per a una avaluació competencial. Si, per contra, l’alumne necessita recuperar els continguts i posar-los al servei de processos matemàtics com ho són la resolució de problemes o l’argumentació, aleshores aquesta activitat té molts números de ser una bona candidata. Aquesta mena de tasques són les que a Innovamat anomenem «riques», i conformen l’eix vertebrador de les nostres propostes.
Tasques avaluables per a secundària
A l’etapa de secundària, proposem un conjunt de tasques avaluables acompanyades de preguntes orientatives per desenvolupar la mirada competencial i ajudar a l’avaluació de continguts i processos. Aquest és un exemple del Tram 1 de 1r d’ESO, que se centra principalment en els nombres naturals (distingir aquests nombres resulta indispensable per fer la tasca):

Què ens permet avaluar una tasca rica com aquesta? Per començar, la consolidació d’alguns coneixements concrets del sentit numèric. Per exemple:
- L'alumne planteja i resol les divisions correctament per obtenir un resultat natural?
- Pel que fa a les operacions combinades, ¿sap que la divisió té prioritat respecte a la suma?
Vegem les respostes d’en Tomàs i en Mohamed:
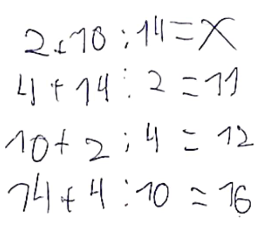
En Tomàs coneix la jerarquia d’operacions entre la divisió i la suma. No obstant això, comet errors molt concrets a l’hora de calcular les divisions. A la tercera operació, en comptes de calcular 2 : 4, ha calculat 4 : 2 = 2. D’aquí que el seu resultat sigui 12. De la mateixa manera, a la quarta línia, deu haver calculat 10 : 4 = 2 (resta 2), n’ha desestimat el residu i ho ha sumat a 14.

En Mohamed no té interioritzada la jerarquia d’operacions. No cal interpretar els seus càlculs, ja que els explicita mitjançant fletxes. D’altra banda, i tenint en compte que es tracta d’un alumne de 1r d’ESO, seria convenient convidar-lo a calcular mentalment les divisions de rangs tan baixos, sense necessitat d’explicitar el càlcul escrit.
Avancem. Què podem observar sobre els processos matemàtics? En una tasca escrita com aquesta, malgrat que l’alumne hagi posat en joc processos diferents, no disposarem sempre d’evidències de tots. En el cas que ens ocupa, sí que hem trobat formes d’avaluar dos d’aquests processos. Comencem per alguns aspectes relacionats amb la resolució de problemes:
- L'alumne és exhaustiu a l’hora de trobar totes les solucions?
- Utilitza una estratègia sistemàtica?

En aquest exemple, la Mikaela demostra una certa sistematicitat, però poca exhaustivitat. Malgrat que, pel que fa a continguts, opera correctament, aconsegueix descobrir únicament 3 solucions de les 6 possibles. On podem observar un indici de sistematicitat? En el fet que ha fixat el 2 com a divisor i ha plantejat primer 10 + 4; després 10 + 14, i finalment 4 + 14. Si hagués considerat l’opció de permutar aquestes parelles de sumands, hauria aconseguit descobrir totes les respostes possibles.

En aquest cas, la Violeta sí que demostra haver utilitzat una estratègia sistemàtica per plantejar les diferents operacions possibles. Ha fixat el 2 com a divisor, el 14 com a segon sumant i ha plantejat les dues possibles operacions amb aquestes condicions. A continuació, ha seguit aquest procediment fixant el 4 com a segon sumant i, finalment, el 10. Com a punt a millorar, podríem convidar-la a justificar per què està segura que no existeixen més solucions amb altres nombres com a divisors.
Per concloure, podríem aprofitar l’apartat b per avaluar el grau d’assoliment del procés de raonament i prova.
- Justifica com ha trobat el resultat més gran i el més petit?

“El resultat més gran és el 12.
El resultat més petit és l’1.”
En aquest exemple, en Pablo ha trobat les respostes correctes, però no observem que justifiqui per què ho són. Simplement, mostra com les ha calculat.

“El més gran: hem sumat els dos nombres més grans (10 + 14) i els hem dividit entre el més petit (2).
El més petit: hem sumat els dos nombres més petits (2 + 4) i els hem dividit entre el nombre més gran (14).”
En Víctor, en canvi, utilitza les propietats de la suma i la divisió per justificar per què els resultats que ha obtingut són, respectivament, el més gran i el més petit. Cal destacar, però, que a l’hora de raonar sobre el nombre més petit, no ha tingut en compte la condició que establia l’activitat: el resultat, en qualsevol cas, havia de ser natural. Ens trobem davant d’un exemple de bon raonament sobre una resposta errònia.
Com veiem, una activitat rica com aquesta permet observar aspectes relacionats tant amb els continguts com amb els processos. La qüestió fonamental ara és: com podem aprofitar totes aquestes observacions per avaluar els nostres alumnes?
Avaluació a Innovamat
Des d’Innovamat defensem que la funció principal de l’avaluació és el seu aspecte formatiu; és a dir, ha de permetre que infants regulin el seu procés d’aprenentatge. En aquest sentit, una cosa que clarament ajudarà els nostres alumnes serà compartir amb ells comentaris com els que hem anat detallant al llarg d’aquest article. Si ho fem, ja els haurem avaluat, que no qualificat.
Paral·lelament, si el que volem és fer servir aquesta tasca per qualificar els resultats del procés d’aprenentatge de l’alumnat (posar notes), podríem utilitzar les diferents qüestions que hem anat desgranant com a indicadors d’avaluació i, si ho considerem oportú, ponderar-los.
Juntament amb aquesta tasca avaluable, a Innovamat oferim dos exemples diferents de resolució de la tasca i unes taules d’avaluació en les quals indiquem quins aspectes han fet bé els alumnes, què podem destacar de la resolució de cadascun dels punts i què poden millorar.
Esperem que recursos com aquesta anàlisi us ajudin, docents, en la difícil tasca d’avaluar els nostres alumnes. Si vols veure un exemple d’avaluació a primària, et deixem aquest article.
- NCTM (2000): Principles and Standards for School Mathematics. Reston, VA, Estats Units
- Sanmartí, N. (2020). Avaluar és aprendre: L’avaluació per millorar els aprenentatges de l’alumnat en el marc del currículum per competències. Direcció General de Currículum i Personalització. Departament d’Educació. Barcelona, Espanya






