Els membres de l’equip didàctic que dissenyem la pràctica digital solem fer observacions d’aula per comprovar com funciona la pràctica en escoles i instituts. En aquest post, compartirem la vivència d’un alumne durant 40 minuts de pràctica digital en una classe de 1r d’ESO en un centre de Barcelona.
Cada dijous a mig matí, l’Eduard i la seva classe de 25 alumnes van a l’aula d’informàtica i fan una estona de pràctica digital. Durant el mes anterior, havien treballat els nombres enters; les últimes sessions que havien fet, concretament, eren la 26 i 27 del Tram 2.
Durant la pràctica digital que vam observar, l’Eduard va practicar el següent:
- 22 operacions multiplicatives amb nombres enters
- 3 operacions combinades amb nombres enters
- 10 operacions combinades amb nombres naturals
- 5 càlculs de potències amb nombres naturals
- 13 estimacions de multiplicacions i restes amb nombres naturals
- 5 estimacions d’arrels quadrades de resultat entre 10 i 20
- 5 càlculs de residu amb calculadora
- 5 càlculs de mitjana i mediana
- 2 tasques de construcció de polígons
- 4 tasques sobre conversions entre g i kg
- 4 construccions de cossos 3D
Treballem la pràctica reproductiva amb l'app
Després d’iniciar sessió, la primera activitat que li apareix és d’operacions multiplicatives. La tasca consisteix a resoldre operacions multiplicatives i additives amb enters, i escriure’n el resultat. L’Eduard dedueix els resultats de les operacions i, a posteriori, escull el signe corresponent. En un parell de situacions ha de demanar ajuda i, en aquests casos, l’activitat li indica el resultat de l’operació equivalent amb nombres naturals. L’objectiu de l’activitat, a banda de saber calcular el valor del resultat, és saber-ne identificar el signe. L’ajuda facilita la primera part. En la línia de l’ajuda, el professor podria preguntar: «Si no et fixessis en els signes dels nombres, quin seria el resultat?» «Ara que ja tens el resultat, torna’t a fixar en els signes, el resultat ha de ser positiu o negatiu?»

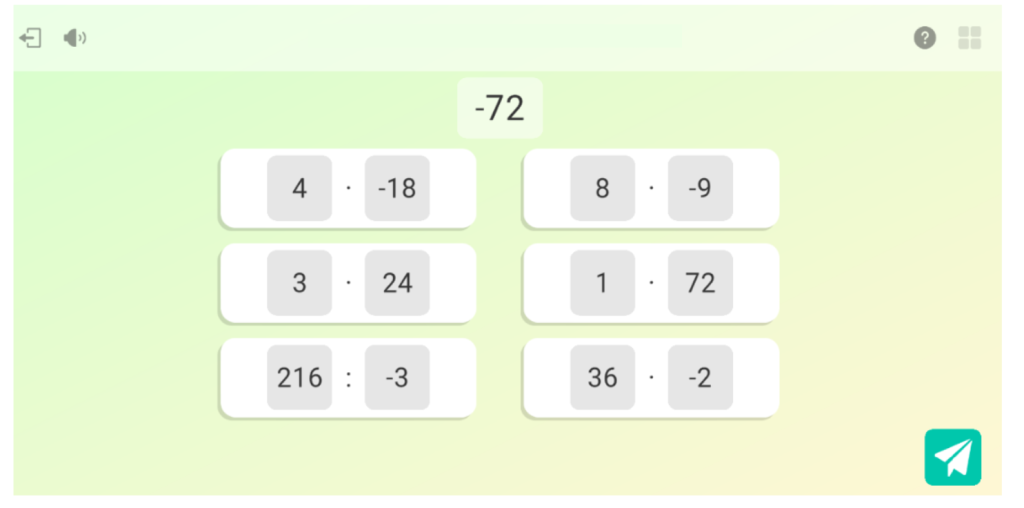
La següent activitat també és d’operacions multiplicatives amb nombres enters, però ara es tracta de seleccionar de manera exhaustiva totes les operacions que tinguin un resultat donat, és a dir, seleccionar les operacions multiplicatives equivalents. L’ajuda, en aquest cas, únicament elimina una opció per reduir la quantitat de càlculs. D’aquesta manera, no s’indica quines s’han seleccionat bé o quines falten per seleccionar, per tal de forçar el càlcul exhaustiu de totes les operacions en pantalla. L’Eduard no indica dues operacions correctes del primer enunciat, però, després de veure’n la correcció, s’adona que les ha de resoldre totes per saber si són possibles solucions. Per agilitzar l’activitat, el professor podria fer veure a l’Eduard que algunes de les operacions es poden descartar sense haver-les de calcular: «Fixa’t en el signe resultant de cada operació, hi ha algun resultat que tingui un signe que no es correspon amb el de l’enunciat?»
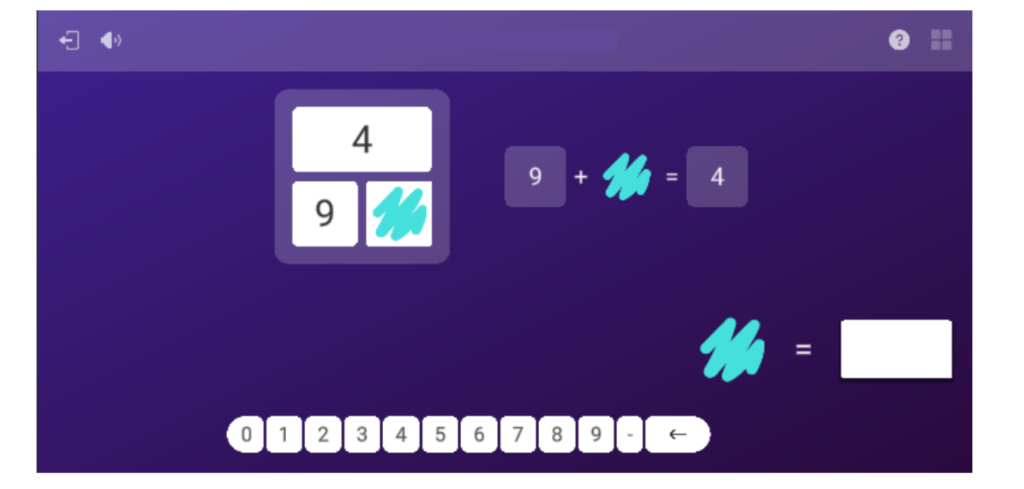
L’Eduard continua amb la resolució d’operacions amb nombres enters. Aquesta vegada, però, són operacions additives i es fa servir la capseta additiva per començar a introduir la resolució d’equacions per cover-up. De fet, l’ajuda que es dona aïlla la taca. En aquesta ocasió, l’Eduard no sap com resoldre-ho i, instintivament, mira l’ordinador de la seva companya. Veu que té la mateixa activitat, però amb nombres diferents. Llavors pregunta què ha de fer i li expliquem el funcionament de la capseta additiva. Una pregunta clau aquí seria: «Quina relació creus que hi ha entre la capseta additiva i l’expressió del costat?»


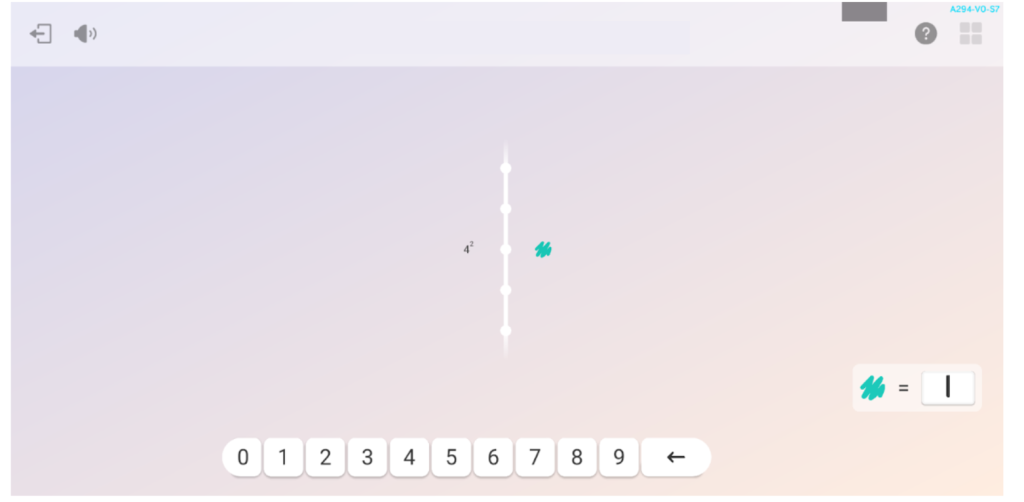
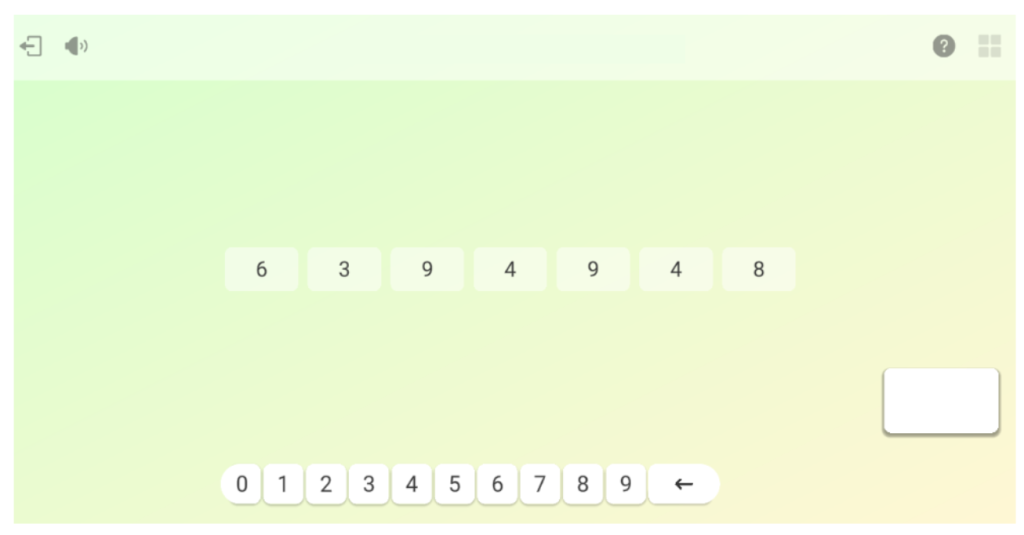

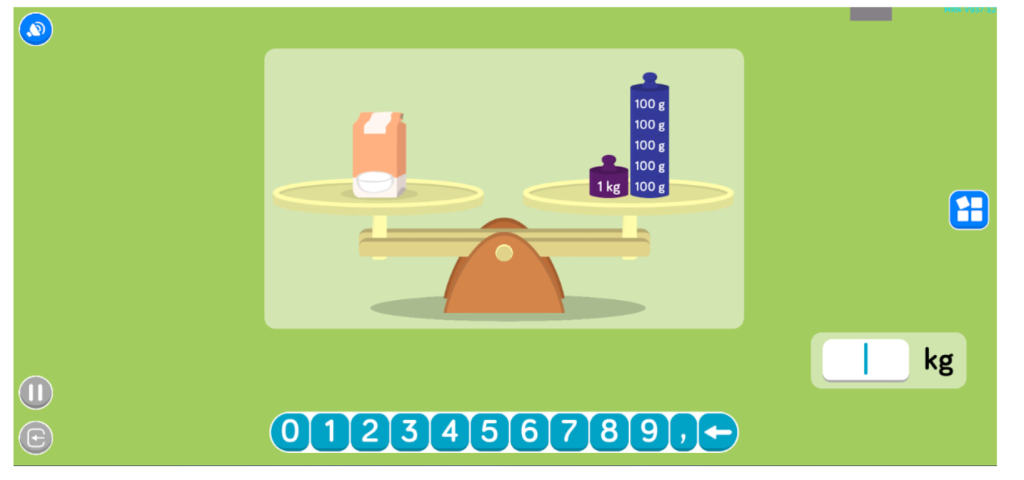
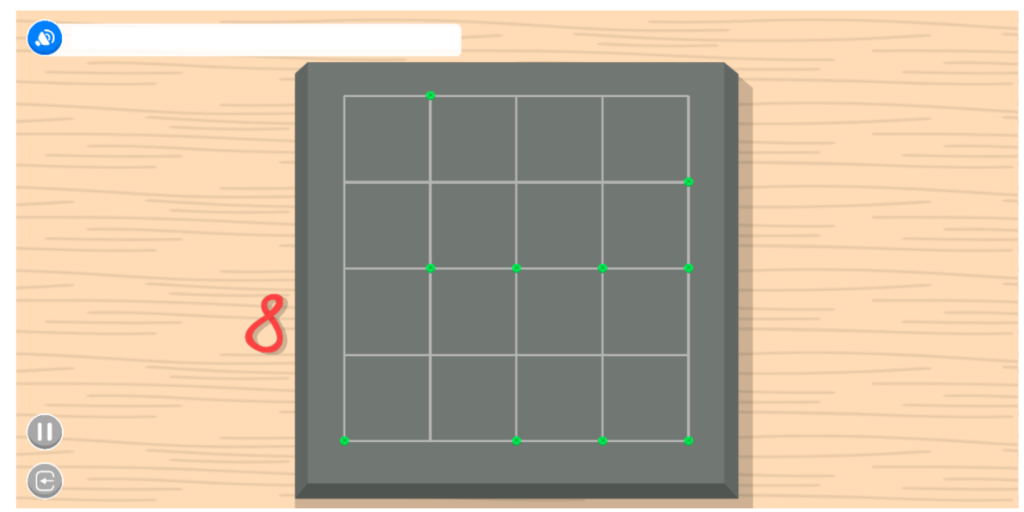

En general, durant tota la sessió es pot percebre la motivació i l’esforç de l’Eduard a l’hora d’enfrontar-se a les activitats. A més, al final de cadascuna rep entre 0 i 3 estrelles, en funció de l’encert que hagi tingut i les ajudes que hagi necessitat. En total avui ha aconseguit 31 estrelles de 42 possibles, així que pot estar-ne prou satisfet.
Tal com expliquem en aquest article sobre la pràctica digital, a partir de l’experiència de l’Eduard podem observar, d’una banda, que la pràctica digital fomenta que l’alumnat estigui més atent i motivat, i que tingui un retorn constant i ajudes i enunciats personalitzats, i, d’altra banda, que el professorat s’estalvia la tasca de corregir (rebrà l’informe detallat a finals de setmana) per concentrar-se a observar més i atendre millor les necessitats de l’alumnat.







