Este mes de diciembre ha estado marcado por la publicación del Informe TIMSS, un documento que ha analizado el rendimiento en matemáticas y ciencias de diferentes países del mundo.
Pero, ¿qué es el TIMSS? ¿Cómo son las pruebas? ¿Qué conclusiones podemos extraer de los resultados? Y, lo más importante, ¿qué podemos hacer los docentes para mejorar la educación matemática?
En este artículo, que adapta una sesión que hicimos en directo, exploraremos todas estas cuestiones y analizaremos didácticamente las pruebas para verlas como oportunidades de aprendizaje. Si prefieres recuperar la sesión, la encontrarás en este enlace.
Descifrando las pruebas TIMSS 2023
Las pruebas TIMSS, del inglés Trends in International Mathematics and Science Study, son exámenes estandarizados internacionales que evalúan las competencias cognitivas en matemáticas y ciencias de los alumnos de 4.º de primaria y 2.º de ESO (4th and 8th grade) de aproximadamente 70 países.
En España, por ejemplo, solo las han realizado los alumnos de 4.º de primaria. Podréis encontrar el informe completo en este enlace. Los países que siguen matemáticas con la propuesta curricular de Innovamat y que han participado en TIMSS son Chile, Brasil, Italia y Estados Unidos. Podréis consultar la lista completa de los países y regiones que han pasado las pruebas TIMSS a través de este enlace.
A partir de estas pruebas, la entidad organizadora IEA (International Association for the Evaluation of Educational Achievement), con la colaboración del Boston College, publica un informe con diferentes conclusiones sobre el rendimiento en matemáticas y ciencias, profundizando en los factores que afectan al aprendizaje. Esta entidad organiza también las pruebas PIRLS (Progress in International Reading Literacy Study), que evalúan la comprensión lectora.
El objetivo principal de estas pruebas es evaluar los sistemas educativos de los diferentes países y extraer conclusiones generales sobre el rendimiento en matemáticas y ciencias del alumnado a nivel global.
Además, el estudio pretende entender los factores que impactan en las habilidades matemáticas y científicas. Para ello, más allá de las pruebas, se pasa un cuestionario al alumnado, los docentes y las escuelas para determinar factores socioeconómicos, bienestar, actitudes y gestión del proceso de aprendizaje del alumnado.
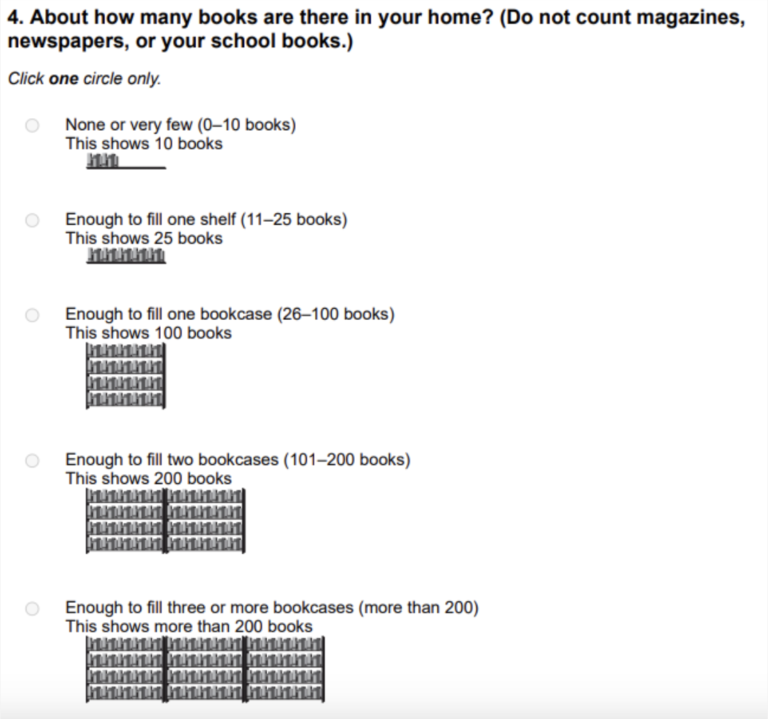
Adjuntamos un extracto de una pregunta del cuestionario dirigido a los alumnos, donde se determina el índice socioeconómico a partir del número de libros que tienen en casa. Si quieres consultar los cuestionarios completos, los encontrarás en este enlace.
¿Qué evalúan las pruebas?
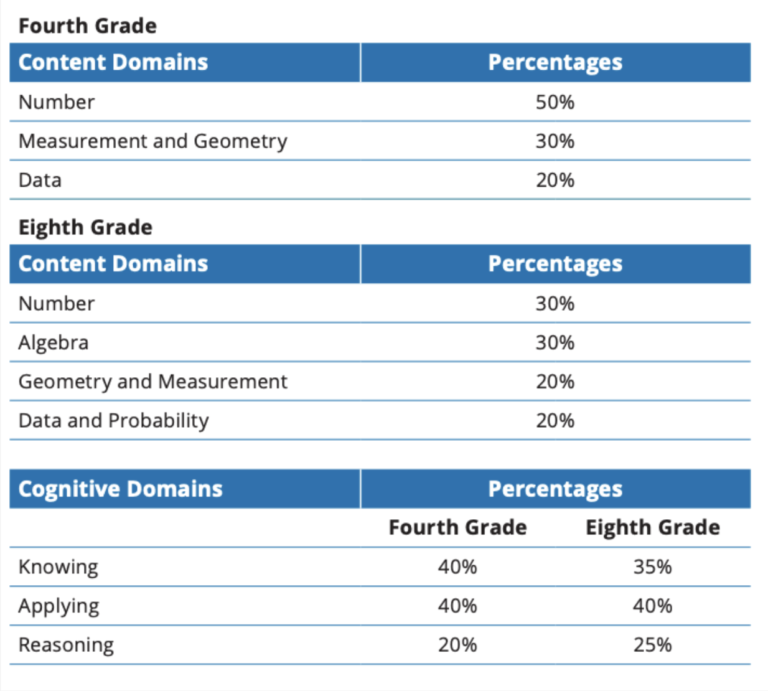
Las pruebas TIMSS evalúan la comprensión y aplicación de los contenidos del currículo. Para hacerlo, se centran en tres dominios cognitivos:
- Conocimiento: ¿Los alumnos recuerdan y comprenden los conceptos matemáticos?
- Aplicación: ¿Saben cómo utilizar este conocimiento en la resolución de problemas?
- Razonamiento: ¿Utilizan el pensamiento lógico y crítico para resolver problemas más complejos?
Podréis encontrar más información sobre los criterios de evaluación aquí.
¿Cómo es la prueba? Comparación con otras pruebas estandarizadas.
Cada alumno responde aproximadamente 50 preguntas de matemáticas y ciencias en poco más de 72 minutos.
Actualmente, solo se han liberado algunos de los problemas, pero analizando la totalidad de la prueba TIMSS 2019 sabemos que son:
- 55% tipo test.
- 41% respuesta numérica.
- 4% respuesta abierta.
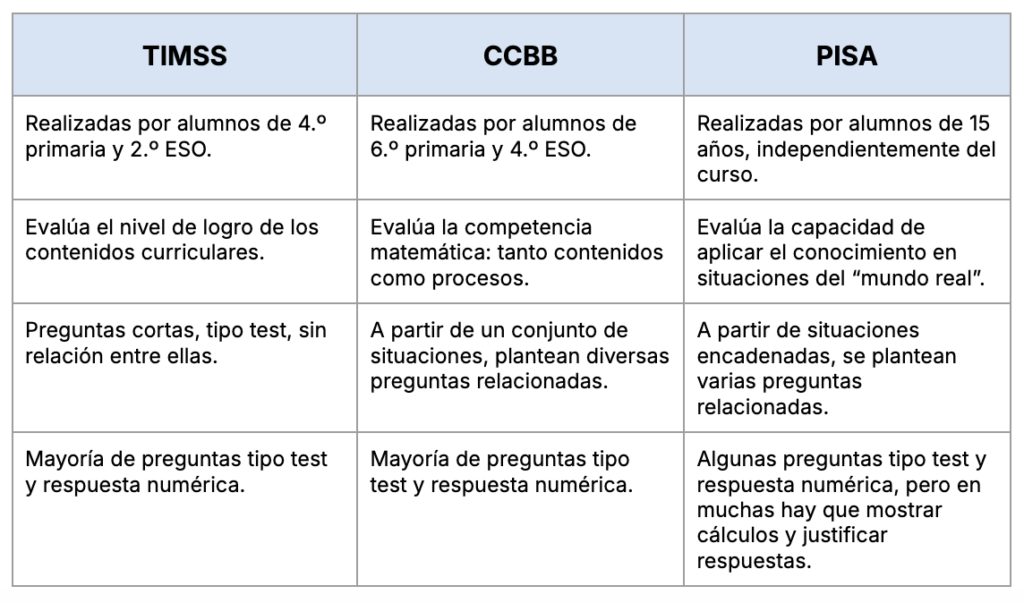
Otras referencias de pruebas estandarizadas son las pruebas de Evaluación de Competencias Básicas en 6.º de primaria y las Pruebas PISA en 4.º de ESO. Comparadas con estas dos pruebas, las diferencias con TIMSS se resumen de la siguiente manera:
Analizamos las pruebas TIMSS 2023. ¿Cómo son las preguntas?
¡Muy bien! Ya hemos visto cómo son las pruebas TIMSS en comparación con otras pruebas estandarizadas. Pero, ¿y los problemas?
Para entender tanto la naturaleza de las preguntas como las condiciones del día de la prueba, y a partir de las pruebas liberadas, decidimos realizar un análisis cualitativo: pasamos las TIMSS a una clase de 4.º de primaria. (Desde aquí, muchas gracias a la Escola Tecnos de Terrassa por abrirnos sus puertas).
Uno de los aspectos que nos llamó la atención fue el factor tiempo. Si los alumnos debían responder 50 preguntas en 72 minutos, esto significaba que tenían aproximadamente 1 minuto y poco más por cada pregunta.
Para contextualizarlo, al mismo tiempo, propusimos las mismas preguntas a adultos, dándoles 1 minuto para responder.

Pregunta 1
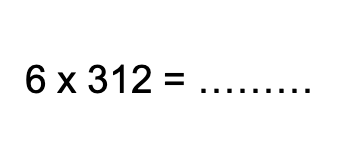
Algunas respuestas de los alumnos:
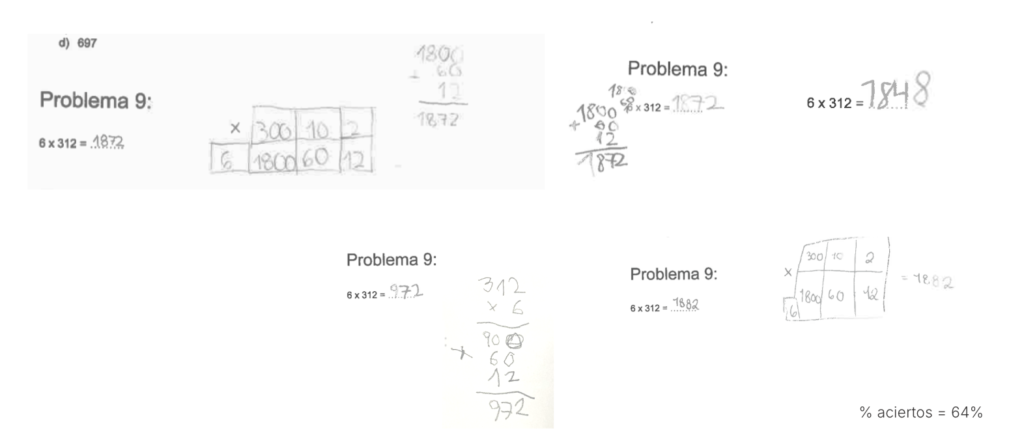
Es interesante observar los diferentes procedimientos seguidos por los alumnos: mientras que unos resolvieron la operación de forma vertical, otros lo hicieron descomponiéndola.
Hay alumnos que, a pesar de realizar correctamente las multiplicaciones, cometieron errores en la suma. Otros, en cambio, se confundieron en la multiplicación, pero hicieron bien el resto de la operación.
Pregunta 2
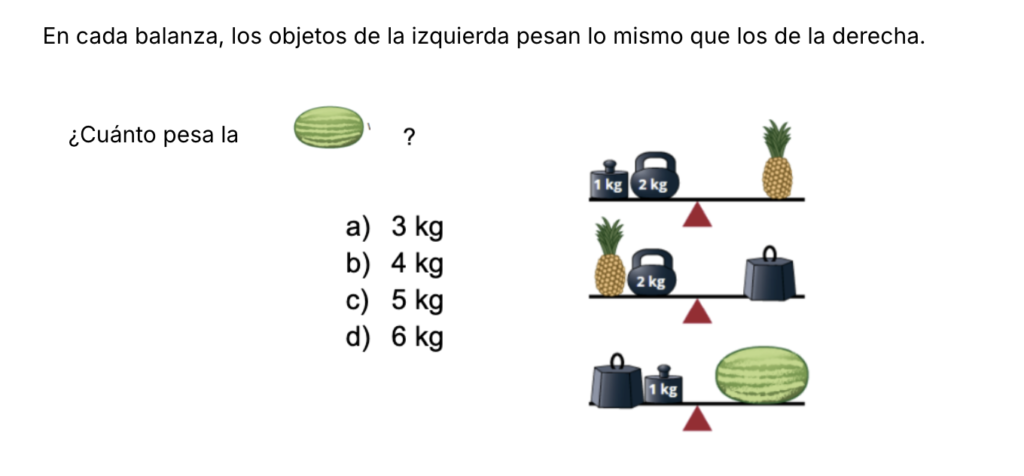
Algunas respuestas de los alumnos:
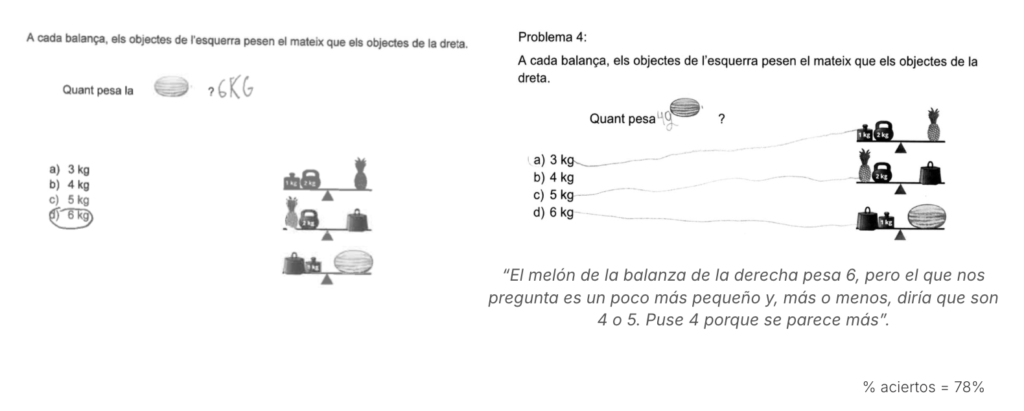
Es una pregunta de preálgebra que requiere deducción y, en general, la mayoría de los alumnos razonó correctamente y llegaron al resultado.
Se han detectado razonamientos originales. Por ejemplo, algún alumno, al ver que la sandía del enunciado era más pequeña que la del ejemplo, asumió que debía pesar menos y aplicó proporcionalidad.
Aunque podemos considerar comprensibles algunos de estos razonamientos (como el segundo ejemplo mostrado en la imagen anterior), la respuesta no se ajusta a los estándares de la prueba y, por tanto, se considera incorrecta.
Pregunta 3
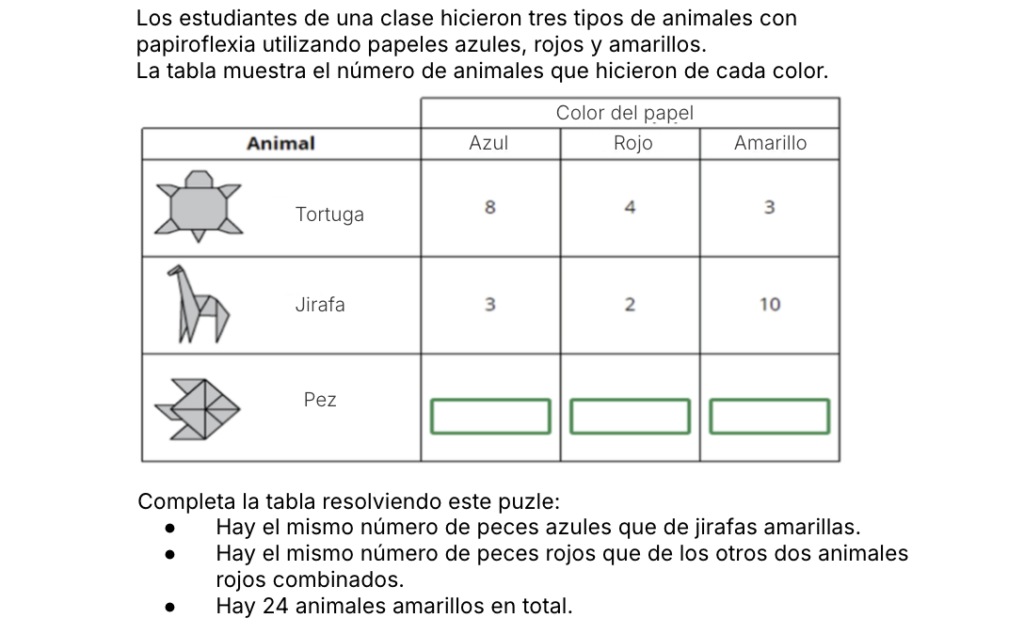
Algunas respuestas de los alumnos:
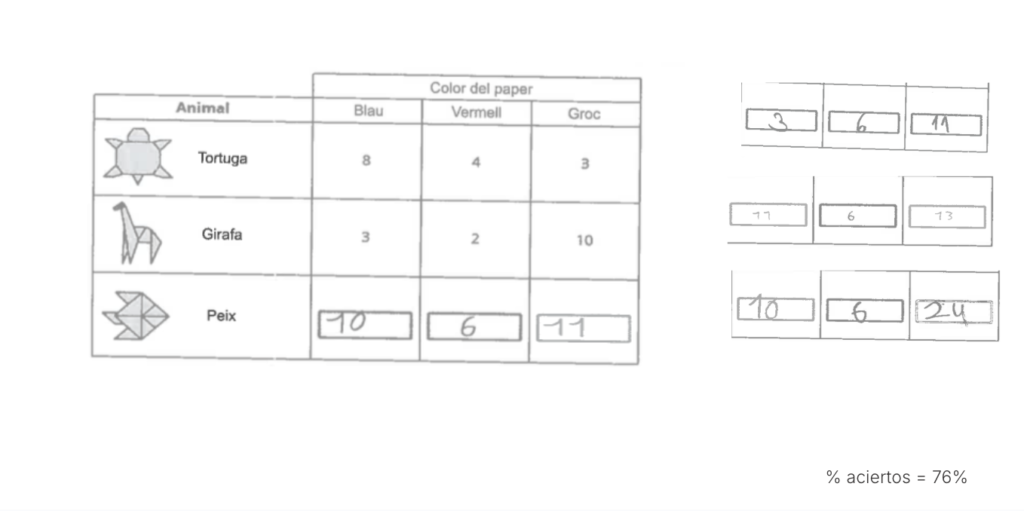
La mayoría de alumnos respondió correctamente. Ahora bien, se han detectado errores en el recuento de peces azules. En este caso, algunos alumnos escribieron “3” porque, en lugar de consultar el número de jirafas amarillas tal como se indicaba, anotaron el número de jirafas azules, que aparecía justo encima de la casilla que debían rellenar.
Un error similar se produjo con el cálculo de los peces amarillos. En vez de realizar la resta indicada —24 menos 3 tortugas amarillas y 10 jirafas amarillas—, los alumnos anotaron directamente “24” como total de peces amarillos.
Consideramos que gran parte de los errores tiene que ver con el factor tiempo, es decir, con una lectura demasiado rápida de los enunciados debido a que contaban con un tiempo limitado para responder las diferentes preguntas. Además, cualitativamente vimos que el enunciado era muy largo y, al tener la tabla en el medio, esto dificultaba la comprensión.
Pregunta 4

Algunas respuestas de los alumnos:

Los criterios de corrección exigían una argumentación. Por este motivo, solo se consideraron válidas las respuestas que justificaban claramente el proceso, por ejemplo: “Sí, todavía puede coger la carta 7 y eso hace que 4+7=11, un resultado superior a 10.”
Si los alumnos se limitaban a decir que sí, porque se podía coger el número 7, sin añadir ninguna explicación adicional, la respuesta no se consideraba correcta.
Pregunta 5

Algunas respuestas de los alumnos:

En este caso, se ha observado un número más bajo de aciertos en comparación con las preguntas anteriores. Muchos alumnos respondieron 150 m o 120 m, mientras que la respuesta correcta era 180 m.
El enunciado hacía referencia a una aproximación, lo que podía resultar confuso para el alumnado, ya que el resultado era exactamente 3 veces y, por lo tanto, la respuesta era exactamente 180 m. Además, existe un posible efecto óptico que puede inducir al error, teniendo en cuenta que la prueba se realizaba en soporte digital, no en papel, y sin regla.
Pregunta 6

Algunas respuestas de los alumnos:

Es una pregunta de operaciones combinadas. En este caso, no se busca que el alumno sepa resolver el problema, sino que, sin haber aprendido este tipo de operaciones en clase, sea capaz de resolver o deducir la respuesta. Es decir, que pueda interpretar las representaciones simbólicas para llegar al resultado.
Un hecho curioso es que aquellos alumnos que plantearon el problema mediante multiplicaciones (en lugar de divisiones) no supieron encontrar la respuesta correctamente, aunque llegaron al resultado correcto a través de su propio razonamiento.
Otros hallazgos interesantes…
Otro problema liberado que pasamos a los alumnos consistía en “redondear”, un concepto trabajado en 4º. No obstante, la principal dificultad radicaba en “redondear al millar”.

En este caso, el alumno escribió el nombre, pero los criterios de evaluación dictan que la respuesta es errónea, ya que se debe responder de forma numérica.
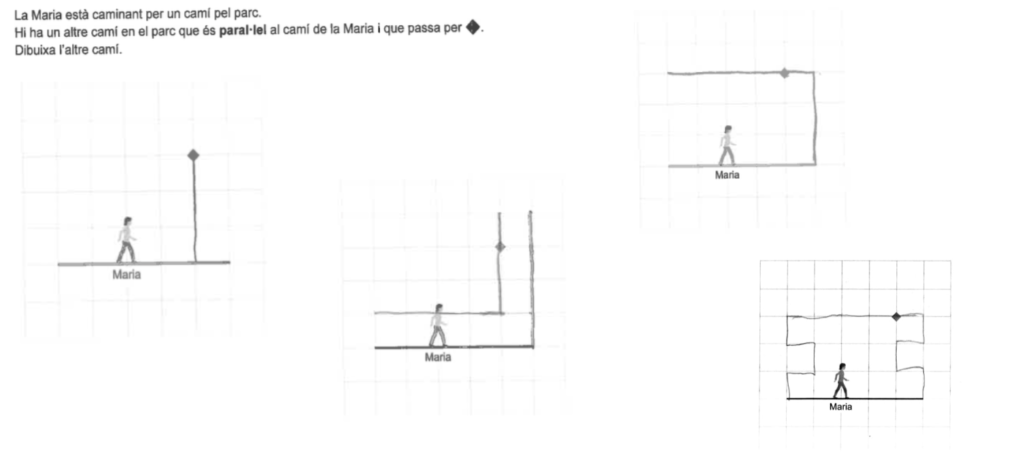
Otra pregunta interesante a nivel de razonamientos era la de dibujar una línea paralela.
En todas estas respuestas podemos observar que los alumnos tienen dominado el concepto de paralelo, pero el contexto les hace representar de forma creativa y crean dibujos, que no serán contados correctamente, ya que solo daban por respuesta correcta la línea paralela que pasaba por el punto.
¿Qué hemos visto?
Después de analizar los problemas, nos fijamos en que los podíamos categorizar de la siguiente manera:
- Aplicación directa de un procedimiento: Por ejemplo, el problema de la multiplicación, donde el alumno debe realizar una operación específica.
- Competencialmente ricos: Como el problema de los animales o el de la sandía, que requieren un razonamiento más complejo.
- Capciosos: Como el problema del edificio, en los cuales es fundamental una interpretación minuciosa del enunciado, ya que puede inducir a confusiones.
- Fuera de nuestro currículo: Como el problema de las pelotas, que sirven para ir más allá de las nociones aprendidas y comprobar la capacidad del alumno para llegar a una conclusión sin tener consolidados los conocimientos específicos.
¿Cómo acabó la dinámica?
Después de la realización de la dinámica, cuando pusimos en común los problemas, el alumnado los había comprendido correctamente. Ahora bien, muchas veces pensamos que imponer presión temporal resulta contraproducente, ya que aumenta el número de errores. Se debe tener en cuenta la variable del tiempo en el análisis de los resultados.

Cuando terminamos la prueba, comentamos los problemas tranquilamente y vimos cómo los alumnos disfrutaban de los diferentes razonamientos y la gran mayoría participaba.
Por eso, es necesario fomentar un aprendizaje que potencie el razonamiento, la reflexión y fomente conexiones. Como maestro, si eres consciente de los puntos en los que los alumnos fallan, los podrás trabajar adecuadamente en clase. Es muy importante darle espacio y tiempo a la conversación en el aula, de manera que el alumno pueda argumentar, explicar razonamientos y detectar dónde y cómo ha fallado, o qué estrategia ha utilizado para resolver el problema. De esta manera, aceptamos que el error es bienvenido y juntos, en dinámica de aula, conseguimos aprender y sacarle provecho a los problemas.
¿Qué nos muestran los resultados?
Después de la publicación del Estudio TIMSS, la prensa y la opinión pública se hicieron eco de unos resultados a la baja. ¡Y es cierto! La tendencia va a la baja. Pero es importante entender los resultados, cómo son las pruebas y las condiciones de los alumnos, y en qué debemos fijarnos.
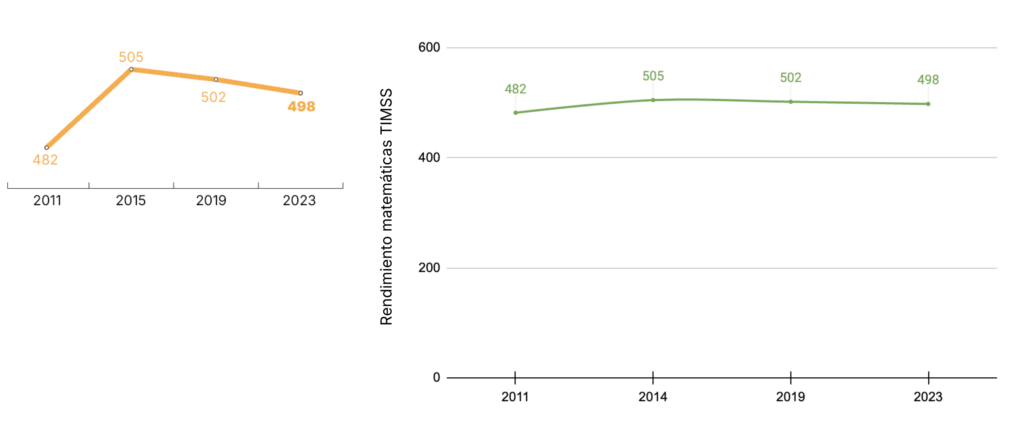
La primera gráfica (de color naranja) muestra la evolución de los resultados de TIMSS en las últimas cuatro ediciones, y a simple vista parece que los resultados han bajado de manera pronunciada.
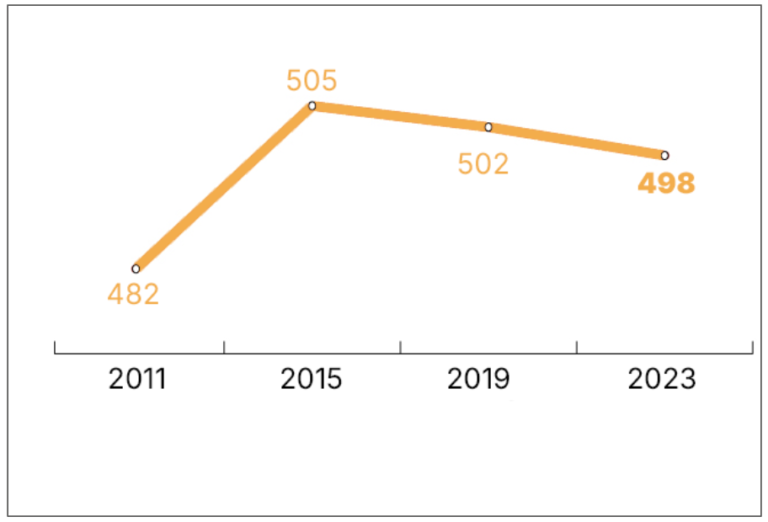
En cambio, si observamos la segunda gráfica (con líneas verdes), que presenta los mismos datos, pero a escala, comprobamos que la variación (-4 puntos) es menos pronunciada de lo que parecía a primera vista en la otra gráfica. Aunque nos gustaría obtener puntuaciones más elevadas, la tendencia de los resultados es bastante estable, aunque a la baja. Se trata de una oscilación moderada dentro de una estabilidad general en los resultados respecto a las ediciones anteriores.
Otro factor que observamos es la gráfica comparativa del rendimiento en matemáticas con el índice socioeconómico de los diferentes países.
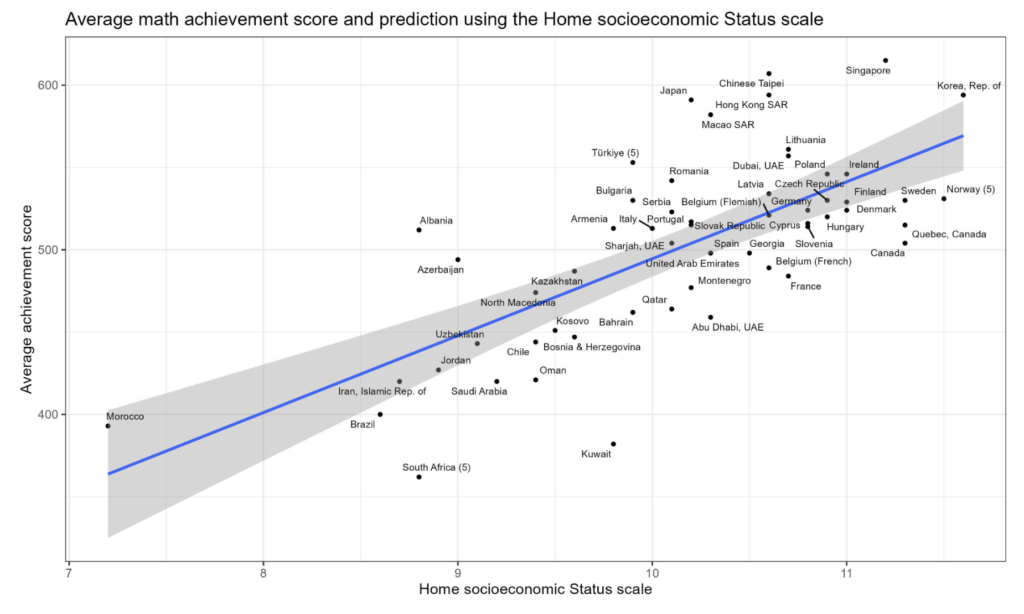
Es importante tener en cuenta la variable socioeconómica a la hora de valorar el nivel de competencia matemática en España.
Observamos que, de acuerdo con el nivel socioeconómico y cultural que tenemos, los resultados no se salen de la normalidad. Esto no quiere decir que debamos conformarnos: debemos apostar por políticas educativas que favorezcan una mejora de los resultados, teniendo en cuenta también que debemos hacer frente a diversos factores que impulsan la tendencia a la baja.
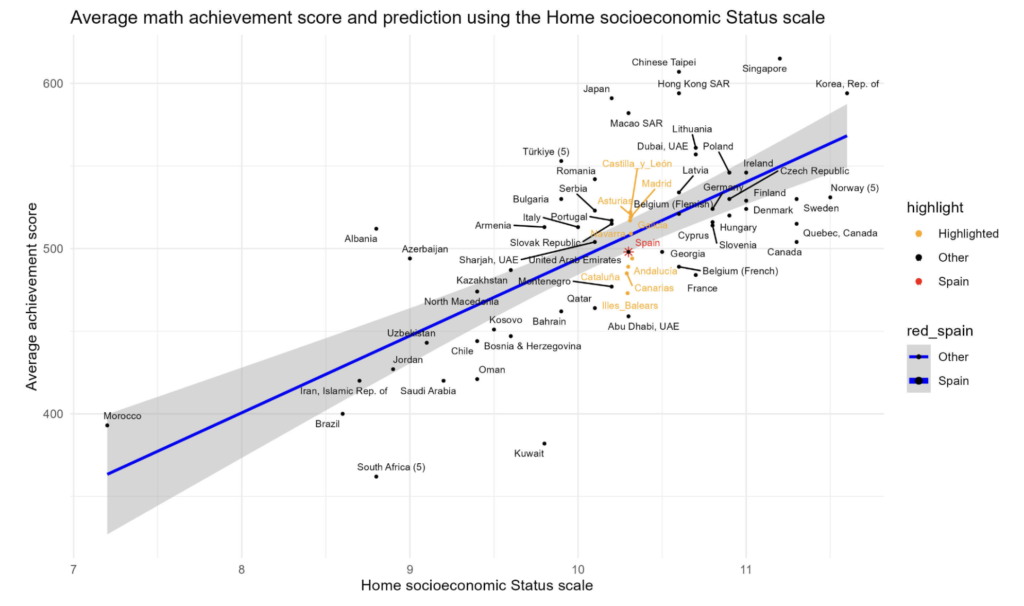
Otra gráfica que trascendió en los medios comparaba los rendimientos en matemáticas de las diferentes comunidades autónomas de España. Hemos querido incorporarlas en el gráfico internacional para ponerlas en perspectiva. De esta forma, podemos observar a escala dónde se ubican respecto al resto de países evaluados.
Otra idea en la que nos queríamos fijar era en los incrementos y los descensos respecto a la prueba anterior, el TIMSS 2019. En esta gráfica vemos qué ha pasado con los bloques de contenido. Observamos que, mientras en algunas áreas los resultados han bajado, en otras se han mantenido o incluso han mejorado ligeramente. Pero las variaciones no son demasiado grandes.
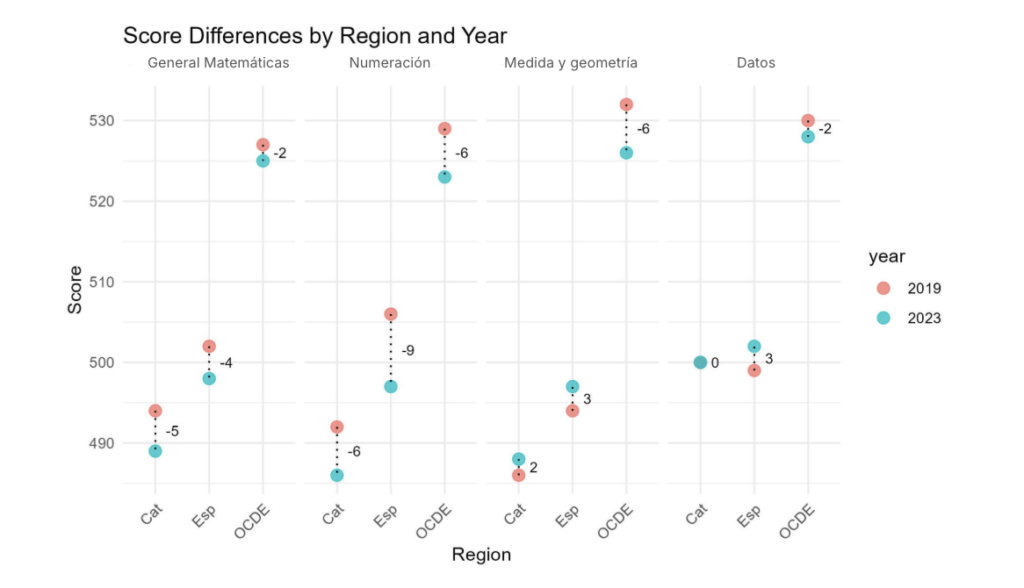
Por otra parte, en lo que respecta a los procesos cognitivos, observamos una mejora de los alumnos catalanes y españoles en razonamiento, mientras que en conocimientos y aplicación hay un ligero descenso de nivel.
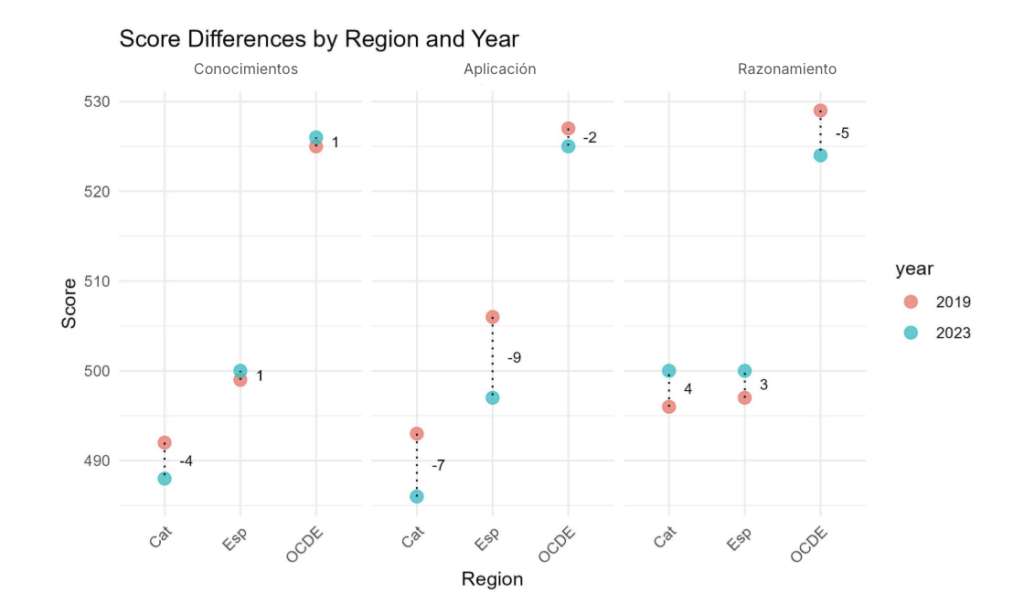
No podemos perder de vista que todas las subidas y bajadas son pequeñas en todos los casos, por lo que se mantiene una cierta estabilidad en los resultados.
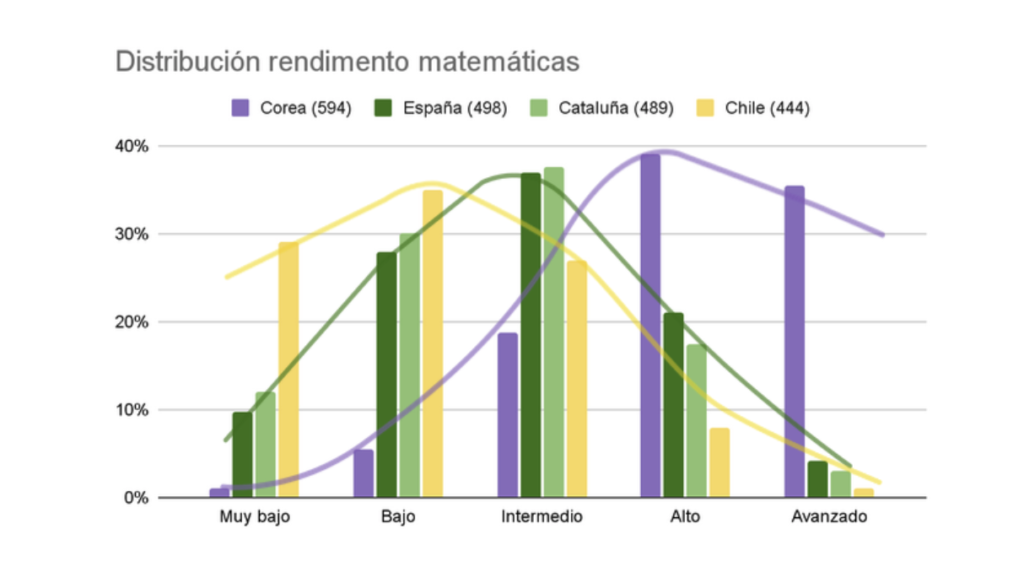
Lo último que quisimos analizar fue cómo se distribuían los alumnos en los diferentes niveles de rendimiento matemático y compararlo entre distintos países. En esta gráfica hemos puesto a España y Chile, que presentan una distribución muy similar, y a Corea, uno de los países con más alumnos en el nivel avanzado. Vemos cómo se mantiene una distribución similar, pero la curva se desplaza hacia la derecha en aquellos países de tradición asiática, como Corea, Japón o Singapur. Podréis encontrar los datos completos en el informe.
¿Qué podemos hacer para mejorar?
Enfrentar los retos educativos actuales requiere ir más allá de la mecanización. No se trata solo de comprender los contenidos, sino de interiorizar los procesos matemáticos para superar los niveles bajos en los resultados.
El aprendizaje competencial, que fomenta el razonamiento, la argumentación y el pensamiento crítico, es clave para afrontar las preguntas de mayor complejidad. Ahora bien, para interpretar los resultados debemos considerar diversos factores, como el contexto socioeconómico de los alumnos.
Ante un problema tan complejo y multifactorial, es esencial sumar esfuerzos desde todos los ámbitos para avanzar en la mejora de la educación y, con ello, de los resultados.
¡Seguiremos, juntos, trabajando para mejorar la educación matemática!





