Los miembros del equipo didáctico que diseñamos la práctica digital solemos hacer observaciones de aula para comprobar cómo funciona la práctica en escuelas e institutos. En este post, compartiremos la vivencia de un alumno durante 40 minutos de práctica digital en una clase de 1º de ESO.
Cada jueves a media mañana, Eduard y su clase de 25 alumnos van al aula de informática y hacen un rato de práctica digital. Durante el mes anterior, habían trabajado los números enteros; las últimas sesiones que habían realizado, concretamente, eran la 26 y 27 del Tramo 2.
Durante la práctica digital que observamos, Eduard practicó lo siguiente:
- 22 operaciones multiplicativas con números enteros
- 3 operaciones combinadas con números enteros
- 10 operaciones combinadas con números naturales
- 5 cálculos de potencias con números naturales
- 13 estimaciones de multiplicaciones y restas con números naturales
- 5 estimaciones de raíces cuadradas de resultado entre 10 y 20
- 5 cálculos de restos con calculadora
- 5 cálculos de media y mediana
- 2 tareas de construcción de polígonos
- 4 tareas sobre conversiones entre g y kg
- 4 construcciones de cuerpos 3D
Trabajamos la práctica reproductiva con la app
Después de iniciar sesión, la primera actividad que le aparece es de operaciones multiplicativas. La tarea consiste en resolver operaciones multiplicativas y aditivas con enteros, y escribir el resultado. Eduard deduce los resultados de las operaciones y, a posteriori, escoge el signo correspondiente. En un par de situaciones debe pedir ayuda y, en estos casos, la actividad le indica el resultado de la operación equivalente con números naturales. El objetivo de la actividad, aparte de saber calcular el valor del resultado, es saber identificar su signo. La ayuda facilita la primera parte. En la línea de la ayuda, el profesor podría preguntar: «Si no te fijaras en los signos de los números, ¿cuál sería el resultado?», «Ahora que ya tienes el resultado, vuelve a fijarte en los signos; ¿el resultado debe ser positivo o negativo?»
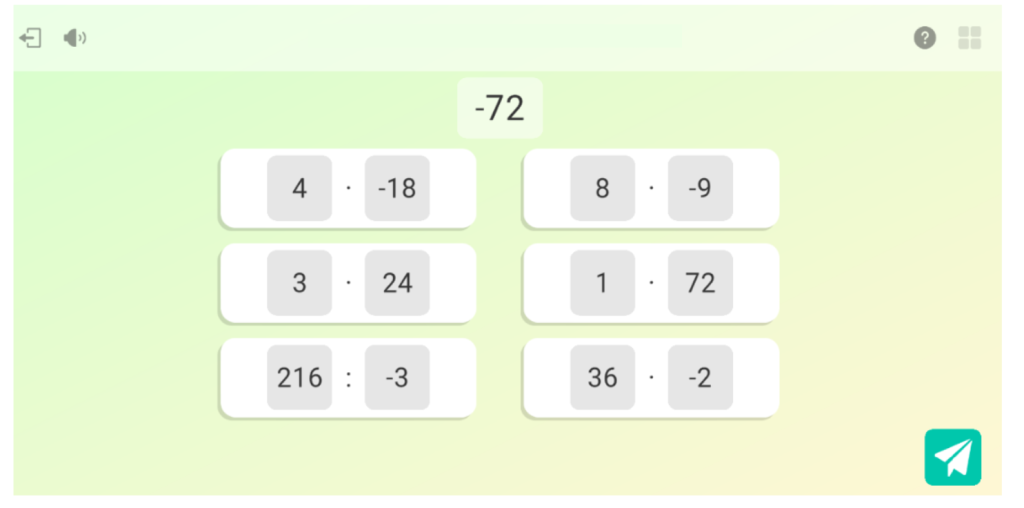
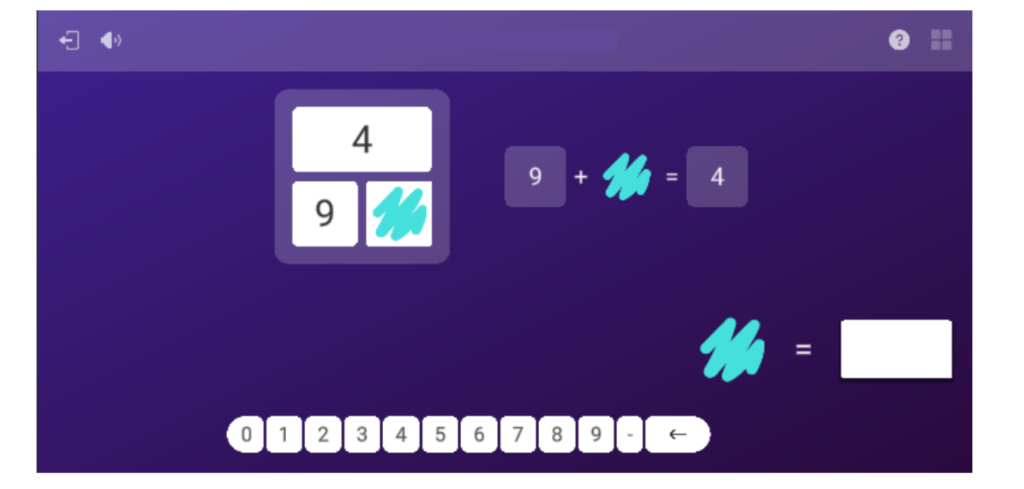
La cuarta actividad es de operaciones combinadas con números enteros. La mecánica consiste en indicar primero la operación a resolver y, seguidamente, su resultado, con el objetivo de hacer énfasis en la prioridad de operaciones e irlas resolviendo poco a poco. Aquí Eduard comenta que le gusta resolver operaciones combinadas con esta actividad, porque «si me equivoco, me lo dice al momento y no se acumula el error hasta el final».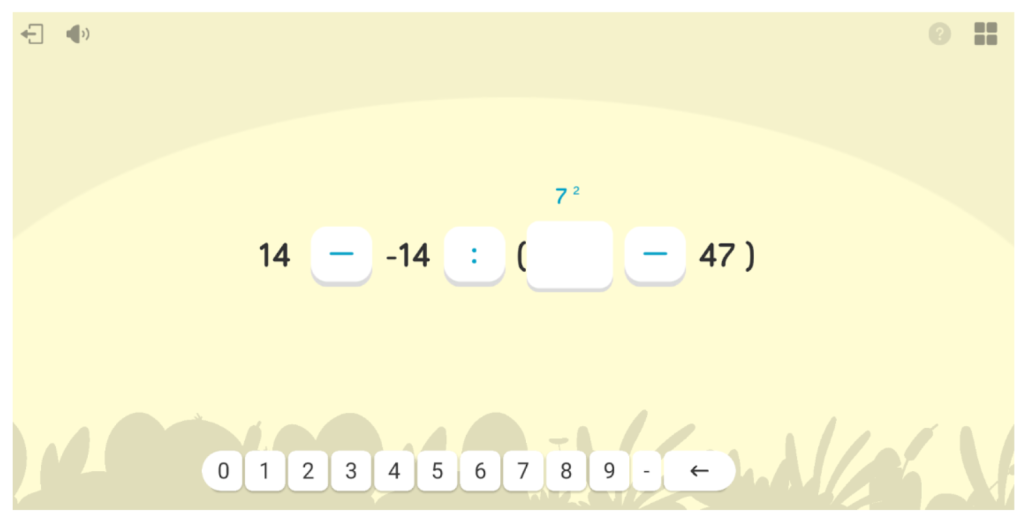
Las actividades siguientes consisten en estimar el resultado de restas, raíces cuadradas y multiplicaciones. Para entender en qué consiste hacer una estimación, una vez resuelta la actividad, se muestra qué error se ha cometido respecto al valor exacto. Hay dos tipologías de actividades: una consiste en colocar la planta en la posición aproximada del resultado, y la otra, en resolver la operación propuesta en un tiempo limitado. Eduard comenta que las actividades que cuentan el tiempo le estresan, pero que, con la práctica, cada vez las hace mejor. En el segundo caso, para fomentar la estimación y evitar la tendencia natural a hacer cálculos exactos, es necesario tener un tiempo límite. Al final de esta actividad, Eduard está contento porque ha obtenido dos estrellas y «eso todavía no lo había conseguido».

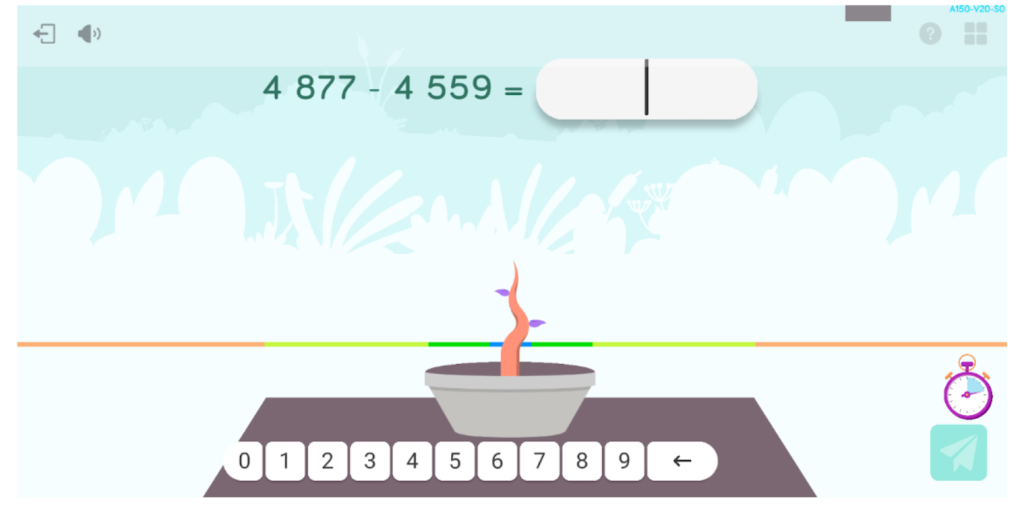

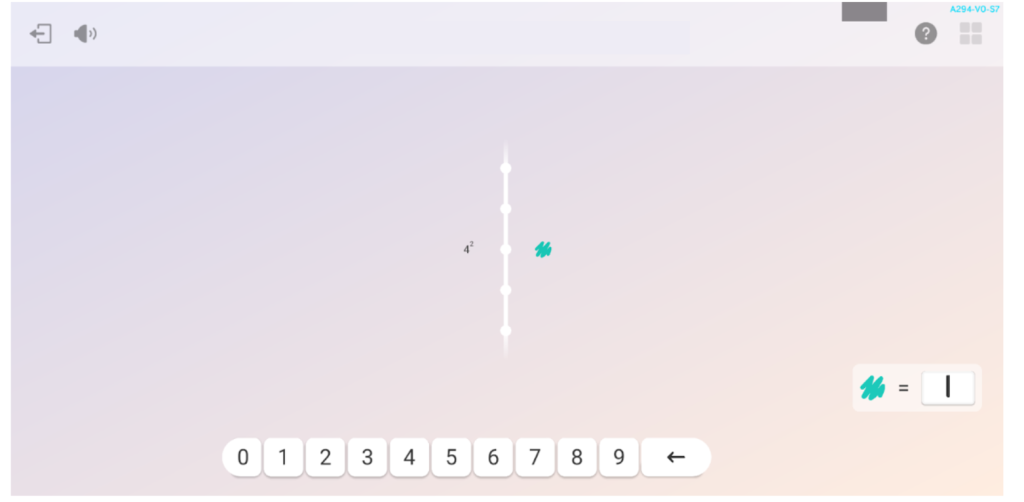

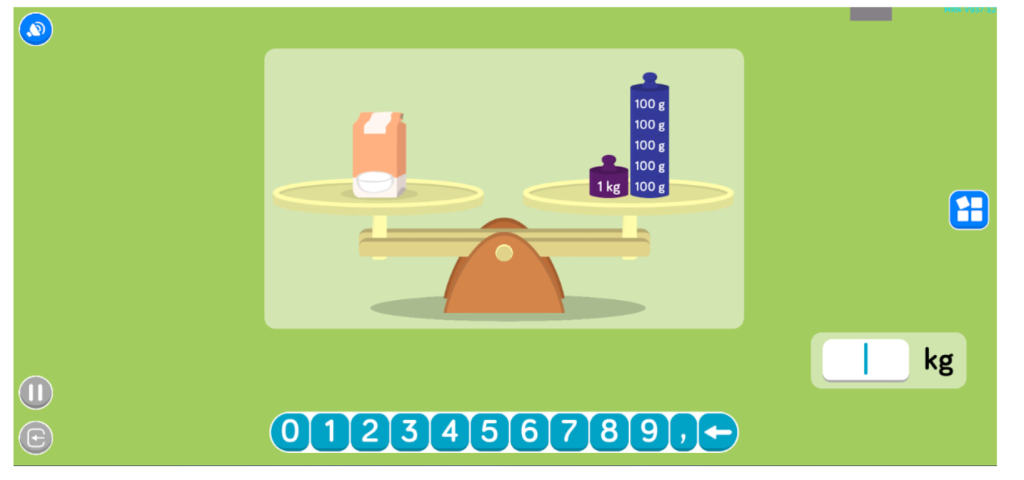
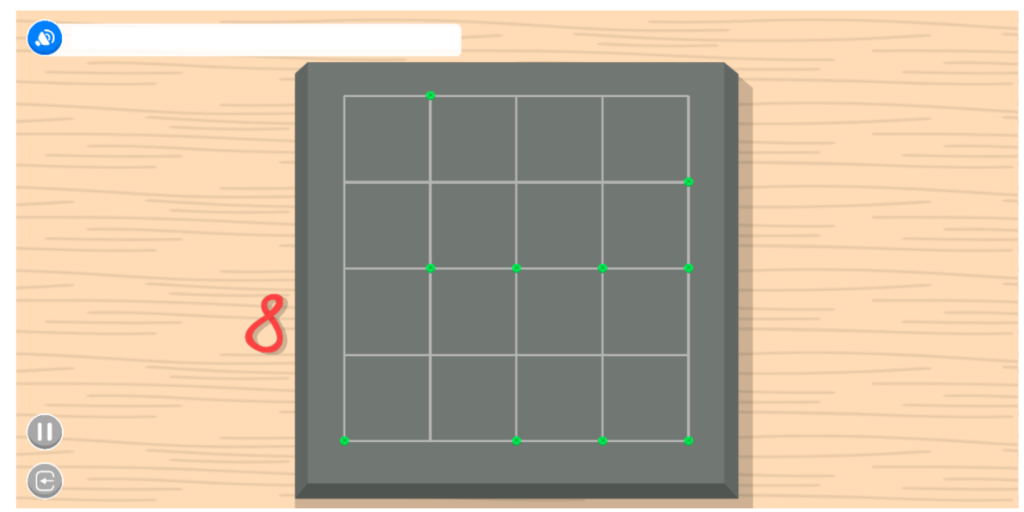

En general, durante toda la sesión se puede percibir la motivación y el esfuerzo de Eduard a la hora de enfrentarse a las actividades. Además, al final de cada una recibe entre 0 y 3 estrellas, en función de los aciertos que haya tenido y las ayudas que haya necesitado. En total hoy ha conseguido 31 estrellas de 42 posibles, así que puede estar bastante satisfecho.
Tal como explicamos en este artículo sobre la práctica digital, a partir de la experiencia de Eduard podemos observar, por un lado, que la práctica digital fomenta que el alumnado esté más atento y motivado, y que tenga un retorno constante y ayudas y enunciados personalizados, y, por otro lado, que el profesorado se ahorra la tarea de corregir (recibirá el informe detallado a finales de semana) para concentrarse en observar más y atender mejor las necesidades del alumnado.







