Download the e-book

- Addition (coming soon)
- Subtraction (coming soon)
- Multiplication (coming soon)
- Division (coming soon)
We know that mathematics is not just about performing operations, but when learning this fundamental aspect, what is more important is understanding what we are doing, getting the correct result, or solving the problems in a reasonable amount of time?
As educators, we should have high expectations for our students’ learning experiences. We must be ambitious!
- Students need to understand what they are doing and why.
- They should be able to achieve correct results by applying procedures accurately.
- Additionally, they should solve operations efficiently within a reasonable timeframe.
As you can see, the answer is not exclusive: all three goals are essential. With this in mind, we recognize that achieving this goal can be challenging. This is especially true in a classroom filled with students who are just beginning their mathematical journey.
In this article, we will explore effective approaches to help students develop fluency in mathematics.
Understand before applying or applying before understanding?
In his book “Building Thinking Classrooms in Mathematics,” Peter Liljedahl proposes 14 practices to promote student engagement and inspire deeper thinking. These practices aim to create classrooms where students are the true protagonists, encouraging them to move beyond mere mechanical repetition.
Why support environments where students perform tasks that a machine can do more efficiently? Instead, when students grasp concepts, such as what it means to subtract or why we use specific strategies like jumps along the number line, they build a stronger foundation for new learning.
With this in mind, focusing on understanding does not mean that students should neglect solving operations correctly; they must still arrive at the correct results. Therefore, classroom time also needs to include practice to consolidate learning and achieve fluency.

In this context, the teacher’s role as a guide is crucial. Teachers should assist students in discovering strategies in a clear and transparent manner. They should also ensure that students consolidate their understanding of the content through practice. This involves encouraging students to step out of their comfort zones and gradually increasing the difficulty of challenges and procedures.
For example, when a student has successfully solved some subtraction problems—using manipulatives as needed—it’s time to encourage them to work without those materials, but instead use visual representations. After they have correctly solved additional problems with this new approach, we should again remove these supports and guide them toward more abstract representations. And so on.
These supports, or scaffolds, are essential in the early stages of learning. However, these supports should gradually fade away, allowing students to achieve more abstract thinking and fluency. The goal is to complete the journey until they can solve operations independently. However, it’s important to have strategies to fall back on if needed.
Building strategies based on the CRA model
What do we understand by fluency?
Fact fluency: smooth recall of known or derived facts through automation. This framework includes the automation to quickly solve single-digit addition problems in the 1st and 2nd grades (e.g., 7 + 3 = 10; 6 + 4 = 10; 8 + 7 = 15) as well as single-digit multiplication in the 3rd and 4th grades (multiplication tables).
Computational fluency: the ability to perform operations (compute) smoothly, beyond simple operations. This framework includes key skills ranging from correctly executing the jump strategy to the sharing model of division.
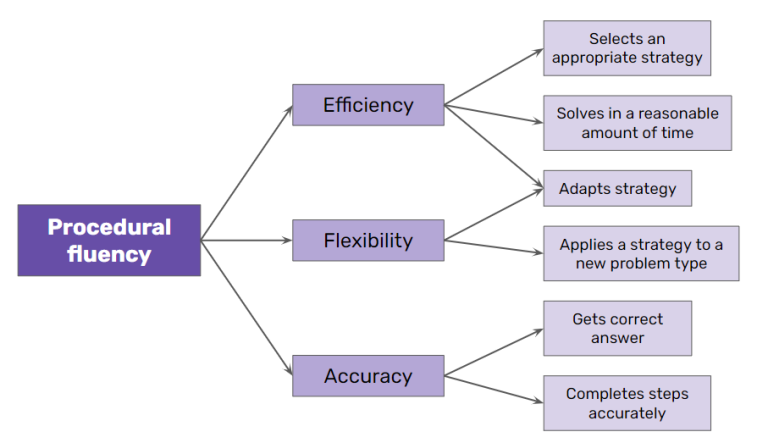
- Procedural fluency: the ability to follow procedures smoothly, going beyond basic operations and depending on the specific stage. This includes finding the lcm, solving combined operations, solving equations, etc.
What facts should be answered quickly?
When discussing learning based on a deep understanding of knowledge, we often overlook the importance of speed in responses. However, certain foundational facts should become part of students’ automatic knowledge. These include:
- The automation of single-digit sums (ranging from 0 to 10)
- The automation of single-digit multiplications (multiplication tables)
These topics fall within the framework of fact fluency. Not being able to respond quickly and, more importantly, lacking efficient strategies to deduce results forces students to spend unnecessary effort on basic calculations. This reduces their ability to focus on more advanced or complex concepts.
Therefore, it is essential to be able to respond quickly, whether by recalling facts from memory or by rapidly deducing them from a few basic results with little effort. For example, a student can quickly deduce that 60 + 70 = 130 by recognizing that 6 + 7 = 13.
How to achieve efficiency and flexibility through building various strategies
As we have seen, one of the pillars for developing fluency is knowing different ways to tackle operations. That is, mastering various strategies that allow us to solve any operation depending on the context and the numbers involved. In short, having flexibility.
Take addition and subtraction as an example. There are instances when using the written algorithm is the most convenient approach. At other times, using mental calculations imagining jumps along the number line is the preferred method. There are also times when we can deduce the result from facts we already know. There are even times when we might choose to use a calculator.
Understanding this variety and being able to select the right strategy enhances our efficiency in calculations. Ultimately, regular practice is essential for gaining speed and agility in executing these operations.
Meaningful learning of basic operations
The learning of mathematics, particularly in the area of numeration, has a hierarchical structure. Mastering one concept is essential to progress to the next. Basic operations—addition, subtraction, multiplication, and division—are fundamental to this process as they serve as the foundation for more advanced numeration and algebraic concepts.
Beyond just learning algorithms, it is important to understand the meaning of each basic operation, know how to solve it, and identify the strategies we can use.
Each operation can be compared to an iceberg: what we see above the water is just a small part of its complexity. The much larger portion beneath the surface represents the understanding and context that support mastery of each operation.
Thus, we have created a resource: a booklet summarizing the learning process behind each basic operation in a succinct and visual manner.
- The meaning of addition, subtraction, multiplication, and division.
- Proposed strategies for solving each operation.
- A learning sequence based on the CRA model that accompanies each strategy.
Download the e-book

References:
Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22-31.
Bay-Williams, J. M., y SanGiovanni, J. J. (2021). Figuring out fluency: Mathematics teaching and learning, grades K-8: Moving beyond basic facts and memorization (1st ed.). Corwin.
Hmelo‐Silver, C. E., Duncan, R. G., y Chinn, C. A. (2007). Scaffolding achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 99–107. https://doi.org/10.1080/0046150701263368
- Van den Heuvel-Panhuizen, M. (2008). Children learn mathematics: Learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Dutch design in mathematics education, V: 1. Utrecht: Freudenthal Institute, Sense Publishers.







