Un exemple d’una tasca rica de 1r de primària
Al més que recomanable treball de Neus Sanmartí (2009) sobre avaluació, l’autora defensa que un dels aspectes que cal revisar primer són les activitats que es proposen per avaluar el nivell d’assoliment de les competències; i que, si se segueix avaluant a través de les tradicionals proves escrites amb preguntes fonamentalment reproductives, no haurà canviat res.
A qualsevol mestre que hagi treballat prou temps en una aula amb alumnes de 6 o 7 anys, aquesta visió li resultarà encara més evident, ja que el grau d’assoliment de la competència lingüística a aquesta edat limita enormement la capacitat de comunicar, argumentar o explicar una estratègia de resolució per escrit. Aleshores, més enllà de les tradicionals proves escrites, com podem obtenir evidències per avaluar competencialment?
Avaluar els processos amb activitats riques
La clau és dominar el marc competencial (és a dir, saber quins processos estem treballant i què esperem del nostre alumnat) i fixar-nos, per exemple, en les seves representacions visuals o gràfiques, o en les seves intervencions durant la conversa a l’aula, sobretot en edats primerenques.
En aquesta línia, hem seleccionat algunes de les activitats riques de la proposta d’Innovamat que considerem especialment adequades per avaluar a través d’aquests mitjans. Aquestes activitats no són les úniques aptes per dur a terme l’avaluació, però proporcionen consells i orientacions sobre com avaluar qualsevol altra activitat rica que, com a docents, considerem oportuna.
Vegem-ho mitjançant un exemple concret, el cas real d’uns alumnes de 1r de primària que van fer una activitat sobre mesura. L’activitat consistia a mesurar la longitud d’alguns objectes representats al quadern mitjançant tres unitats de mesura diferents: dits, cubets i una tercera unitat que podien escollir ells.

Què podem avaluar en una activitat com aquesta? Per començar, el comptatge resultatiu de l’1 al 20 i l’escriptura d’aquests nombres, que són continguts tan necessaris que, si no es dominen, tota l’activitat es veu condicionada.

En aquest cas, observem algunes respostes amb nombres excessius, com ara «30 llapis» o «54 dits». És possible que el problema d’aquest infant tingui a veure amb el sentit numèric, més que amb el de la mesura.
Podem preguntar-li com es llegeixen aquests nombres, i si són més grans o més petits que altres de referència.
A més, és evident que els infants hauran de posar en joc alguns coneixements concrets del sentit de la mesura. Per exemple:
- Utilitza una tècnica de mesura precisa quan mesura amb els dits?

En aquest cas, l’infant concatena els índexs de les dues mans, orientats de forma perpendicular a l’objecte, cosa que li permet ser consistent i obtenir sempre la mateixa mesura.

En canvi, en aquest cas l’infant només fa servir un dit índex per anar «saltant» sobre l’objecte. En fer-ho així, perd la referència del punt exacte fins al qual havia mesurat i, quan torna a col·locar el dit, deixa espais o torna a mesurar un espai ja mesurat.
Podem indicar-li que aquesta tècnica és poc precisa i que pot provocar que, quan torni a mesurar el mateix objecte, obtingui un resultat diferent, fins i tot si fa servir el mateix dit i la mateixa tècnica.
Li podem preguntar: «Com pots estar segur que quan aixeques el dit i el tornes a col·locar no l’has posat al mateix lloc que abans?»
Seguim! De les diferents tasques implícites en aquesta activitat, clarament la més competencial és la que té a veure amb escollir la unitat de mesura amb criteri. Ens podem plantejar:
- L'infant s'assegura d'escollir com a unitat de mesura un objecte que sempre tingui la mateixa longitud?

Aquí, l’infant fa servir una goma d’esborrar sense canviar-ne l’orientació.

Aquí, en canvi, mesura amb targetes numèriques plastificades. En alguns moments, mesura tenint en compte el marge plastificat, i en d’altres, mesura només amb la part blanca de la targeta, prescindint del marge de plàstic.
Podem fer-li veure la incongruència si li demanem que torni a mesurar el mateix objecte i li preguntem si ha obtingut el mateix resultat.
Per altra banda, aquesta activitat requereix algunes habilitats pròpies dels processos matemàtics. Pel que fa a Resolució de problemes, podríem plantejar:
- Quan se li demana que esculli una unitat de mesura, troba una solució òptima?
En aquest cas, és interessant destacar que el concepte «òptim» es pot matisar en funció del criteri de l’infant. Què pretenia: ser precís o ser eficient? O totes dues coses?
Vegem-ne un parell d’exemples diferents:

Aquest infant ha triat una goma d’esborrar. En fer-ho, ha pogut ser precís (referint-nos només a l’element i no a la tècnica, que també afectarà el grau de precisió), ja que la unitat de mesura cap diverses vegades en la longitud de l’objecte mesurat. A més, ha enregistrat «4 i mig» al seu quadern.

Aquest infant, en canvi, ha seleccionat un llapis, cosa que li ha permès ser més eficient: només ha necessitat un mesurament per donar la resposta.
En tots dos casos seria pertinent preguntar-los quin criteri han seguit i plantejar-los com ho farien per considerar un criteri diferent.
Això també està relacionat amb la Resolució de problemes. Ens podem preguntar:
- Comprova que la solució que ha obtingut és raonable?

Sense entrar a valorar la precisió de les mesures preses, podem observar que les respostes són raonables pel que fa a la relació entre elles.
Les respostes expressades en dits i cubets són coherents amb el fet que, a cop d’ull, es veu que la sargantana és l’element més llarg, i el centpeus, el més curt.
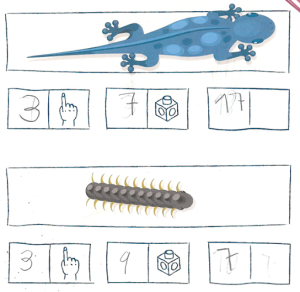
En aquest cas, no és raonable que dues il·lustracions que, a cop d’ull, tenen longituds clarament diferents mesurin el mateix (3 dits). La resposta resulta encara més il·lògica quan veiem que les longituds mesurades amb cubets són diferents.
Seria interessant fer-ho evident formulant preguntes i guiant l’infant perquè es plantegi la importància de revisar els resultats.
Per acabar, podríem plantejar algunes preguntes per diagnosticar el grau d’assoliment del procés de Raonament i prova:
- És capaç de justificar per què mesura d’una manera en particular?

Aquest infant, per mesurar amb els dits, utilitza els 5 alhora. Podem preguntar-li per què ho fa.
Podria no saber-ho justificar o, per contra, podria raonar que, així, mesurarà de forma més ràpida.
I una última relacionada amb Raonament i prova:
- L’alumne observa que mesurar amb cubets és més fiable que amb els dits?
Com dèiem al principi, demanar a un infant de 6 o 7 anys que deixi per escrit un raonament pot no ser la millor manera d’avaluar els processos. Per això, hem de tenir molt en compte la possibilitat d’avaluar també les converses que es generen a l’aula:

Un altre gran potencial de la conversa a l’aula és que, en cas que un infant respongui de manera poc explícita, el docent pot gestionar la conversa en aquell mateix moment per esbrinar de manera més clara el que l’infant raona en realitat.
Avaluació a Innovamat
Des d’Innovamat defensem que la principal funció de l’avaluació és el seu aspecte formatiu; és a dir, ha de permetre als infants regular el seu propi procés d’aprenentatge. En aquest sentit, una cosa que clarament ajudarà els nostres alumnes és compartir amb ells comentaris com els que hem anat detallant al llarg d’aquest article. Si ho fem, ja els haurem avaluat, que no qualificat.
Paral·lelament, si el que volem és fer servir aquesta tasca per qualificar els resultats del procés d’aprenentatge (posar notes), podríem utilitzar les diferents qüestions que hem anat desgranant com a indicadors d’avaluació i, si així ho considerem oportú, ponderar-los.
Com hem vist, saber què podem observar a cada moment i tenir a mà alguns exemples de respostes reals de l’alumnat són recursos que ens poden ajudar molt en la difícil tasca d’avaluar.
- NCTM (2000): Principles and Standards for School Mathematics. Reston, VA, Estats Units
- Sanmartí, N. (2020) Avaluar és aprendre: L’avaluació per millorar els aprenentatges de l’alumnat en el marc del currículum per competències. Direcció General de Currículum i Personalització. Departament d’Educació. Barcelona, Espanya






