S’han de saber les taules de multiplicar de memòria? Cal fomentar l’esforç en matemàtiques? I la pràctica, és important?
Aquestes són algunes de les preguntes que ens feu arribar sovint; i no hem volgut perdre l’ocasió de convertir-les en un joc.
Estàs a punt?
1/5 Ha canviat la manera de fer les operacions bàsiques?
Fem les operacions de la mateixa manera, el que canvia és com les aprenem.
Perquè l’alumnat tingui fluïdesa en la resolució d’operacions i arribi al resultat correcte de manera eficient, cal construir-les fomentant-ne una comprensió profunda: què estem fent i per què funciona?
Per construir amb significat les operacions bàsiques (sumes, restes, multiplicacions i divisions), es presenten diferents estratègies. El domini de les diferents estratègies, a més d’augmentar la comprensió, afavoreix la flexibilitat en els càlculs.
Cadascuna d’aquestes estratègies té un procés d’aprenentatge dissenyat per maximitzar aquesta comprensió. Comencem pel més concret, utilitzant materials manipulatius, fins a arribar al més abstracte, aconseguint-ne una representació més eficient i compacta.

- Van Den Heuvel-Panhuizen, M. (2008). Children Learn Mathematics: A Learning-Teaching Trajectory with Intermediate Attainment Targets for Calculation with Whole Numbers in Primary School. Dutch Design in Mathematics Education, Vol. 1. Utrecht: Freudenthal Institute, Sense Publishers.
Kilpatrick, J., Swafford, J., Findell, B., & National Research Council (U.S.), Mathematics Learning Study Committee. (2001). Adding it up: Helping children learn mathematics. National Academy Press.
2/5 És important practicar?
La pràctica és essencial per consolidar els coneixements i guanyar fluïdesa.
Per això, és important dedicar moments a la pràctica reproductiva: enfocada a assolir el domini d’un procediment concret mitjançant la repetició d’aquest. I, moments a la pràctica productiva, on la pràctica esdevé una excusa per posar en joc els processos matemàtics, com la resolució de problemes.
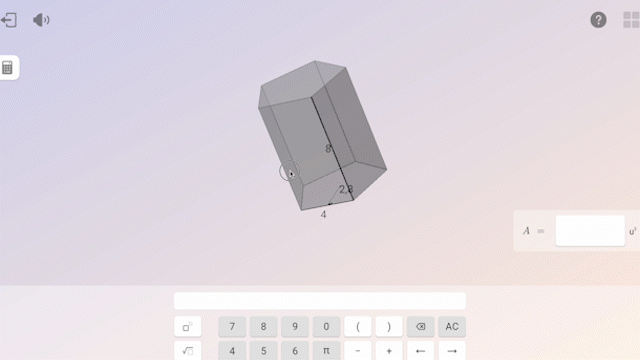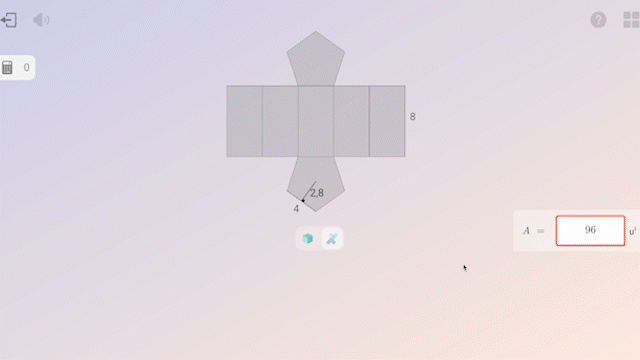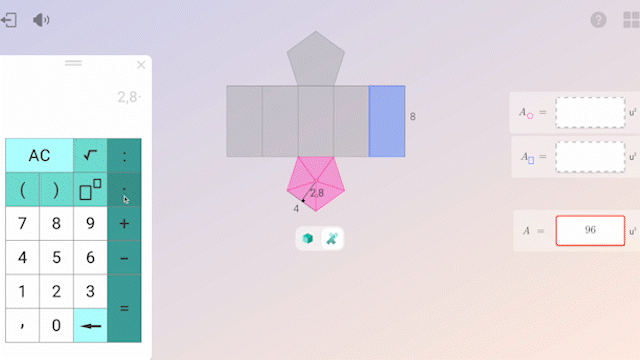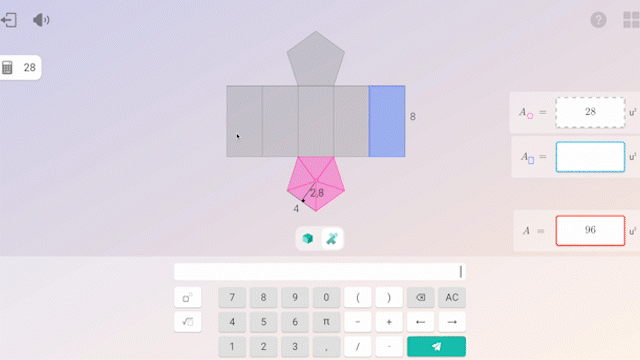
L’ús de la tecnologia en la pràctica aporta un valor afegit: permet individualitzar l’aprenentatge, oferint retorn immediat i informes detallats sobre el progrés de cada alumne. Això permet que els docents puguem ajustar l’acompanyament a cada estudiant.

- Spangler, D. A., & Wanko, J. J. (2017). Enhancing Classroom Practice with Research Behind Principles to Actions. NCTM.
Pettersson, F. (2017). On the issues of digital competence in educational contexts – a review of literature. Education and Information Technologies, 23(3), 1005–1021. https://doi.org/10.1007/s10639-017-9649-3
3/5 Les taules de multiplicar s’han d’acabar sabent de memòria?

L’automatització de les taules és imprescindible per aconseguir aprenentatges significatius en conceptes posteriors, com per exemple les divisions o les potències.
Després de la construcció de les taules de multiplicar, és el moment de practicar-les perquè l’alumnat n’automatitzi els resultats i tingui estratègies per deduir ràpidament aquells que, encara, no se sap de memòria.
El fet de no saber-se-les, augmenta la càrrega cognitiva en problemes avançats, ja que els alumnes han de dedicar esforç a càlculs bàsics, reduint la seva capacitat per concentrar-se en altres aspectes més complexos.
Bay-Williams, J. M., & SanGiovanni, J. J. (2022). Accessing Fluency through Routine and Opportunity. NCTM Annual Meeting 2022. Los Angeles.
Vilalta, A., Calvo, C., & Correig, E. (2023). Automatizar las tablas de multiplicar: un propósito que va más allá de 3.º EP. UNO: Revista de Didáctica de las Matemáticas, 99, 61-67.
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257-285.
4/5 S’han de plantejar unes matemàtiques que s’aprenguin sense esforç?

L’esforç en l’aprenentatge de les matemàtiques no s’ha d’evitar, sinó que cal aprofitar-lo per aprendre. Parlem d’esforç productiu (de l’anglès productive struggle), que consisteix a desenvolupar perseverança i flexibilitat de pensament, en lloc de simplement buscar la solució correcta.
Els docents, ajustem aquest esforç plantejant reptes adequats, sense donar respostes directes, i fomentant la motivació i l’autonomia dels alumnes.
Tenir una mentalitat de creixement és fonamental per veure els errors com a oportunitats per avançar en el procés d’aprenentatge, desenvolupant resiliència i mantenint la motivació.
- Boaler, J. (2016). Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages, and Innovative Teaching. Jossey-Bass.
Dweck, C. S. (2006). Mindset: The New Psychology of Success. Random House.
5/5 Nosaltres, com a docents, tenim un paper rellevant en tot això?

Cap recurs o material, per ben dissenyat que estigui, pot tenir èxit sense la dedicació i experiència dels docents.
No hi ha fórmules màgiques: el vostre compromís, formació contínua i confiança en el potencial dels alumnes són els veritables motors del seu aprenentatge.
Per això, les guies didàctiques i les oportunitats de formació són eines valuoses que podeu aprofitar per continuar creixent com a professionals i oferir la millor experiència possible als vostres alumnes.
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22.
Darling-Hammond, L. (2000). Teacher quality and student achievement: A review of state policy evidence. Education Policy Analysis Archives, 8(1), 1-44.
Si us ha despertat curiositat, us animem a consultar el nostre llibre blanc, on explorem a fons aquestes i altres qüestions.
Estem aquí per donar-vos suport i treballar junts per impulsar l’aprenentatge matemàtic de l’alumnat.
A reveure!






