Praktika digitala didaktika taldean diseinatzen dugu, eta horretan aritzen garen taldekideok ikasgelako behaketak egin ohi ditugu praktikak eskola eta institutuetan nola funtzionatzen duen egiaztatzeko. Artikulu honetarako, behaketa egin genion DBHko 1. mailako ikasle bati hura 40 minutuz praktika digitalean aritu bitartean.
Ostegunero, goizerdi aldera, Eduard eta bere gelako gainerako 24 ikasleak informatika-gelara joaten dira eta praktika digitala egiten dute. Aurreko hilabetean zenbaki osoak landu zituzten; zehazki, egin zituzten azken saioak 2. ataleko 26. eta 27. saioak izan ziren.
Behatu genuen praktika digitaleko saioan, Eduardek honako jarduera hauek egin zituen:
- Zenbaki osoen arteko 22 eragiketa biderkatzaile
- Zenbaki osoen arteko 3 eragiketa konbinatu
- Zenbaki arrunten arteko 10 eragiketa konbinatu
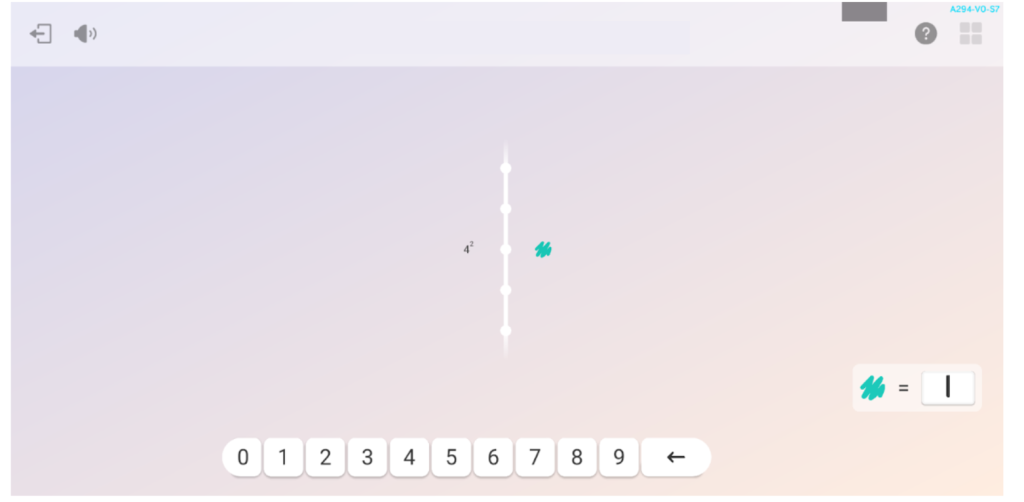
- 5 berreketa zenbaki arruntekin
- Zenbaki arrunten arteko 13 biderketa eta kenketaren zenbatespenak
- Emaitza 10 eta 20 artekoa duten 5 erro karraturen zenbatespenak
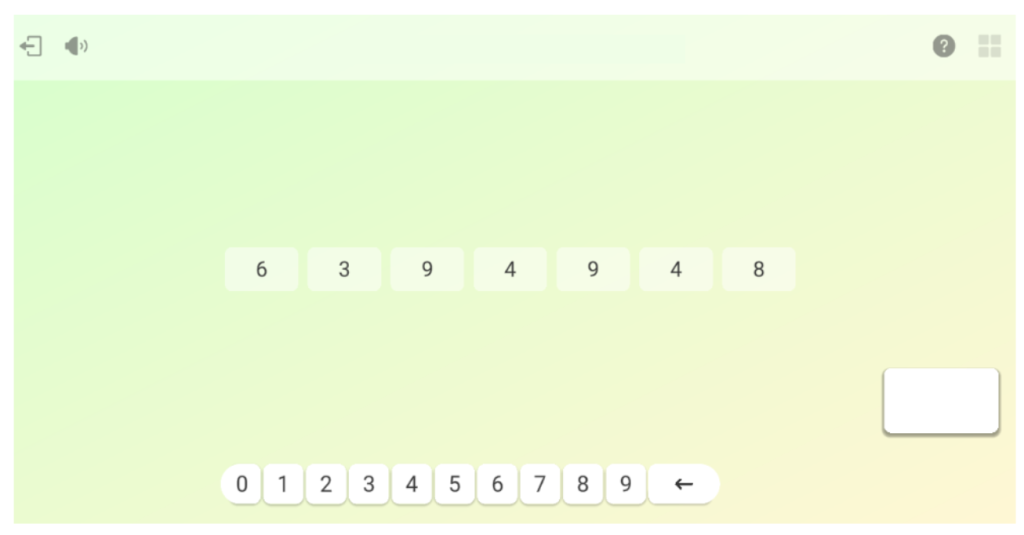
- 5 hondar kalkulatzea kalkulagailuarekin
- 5 batezbesteko eta mediana kalkulatzea
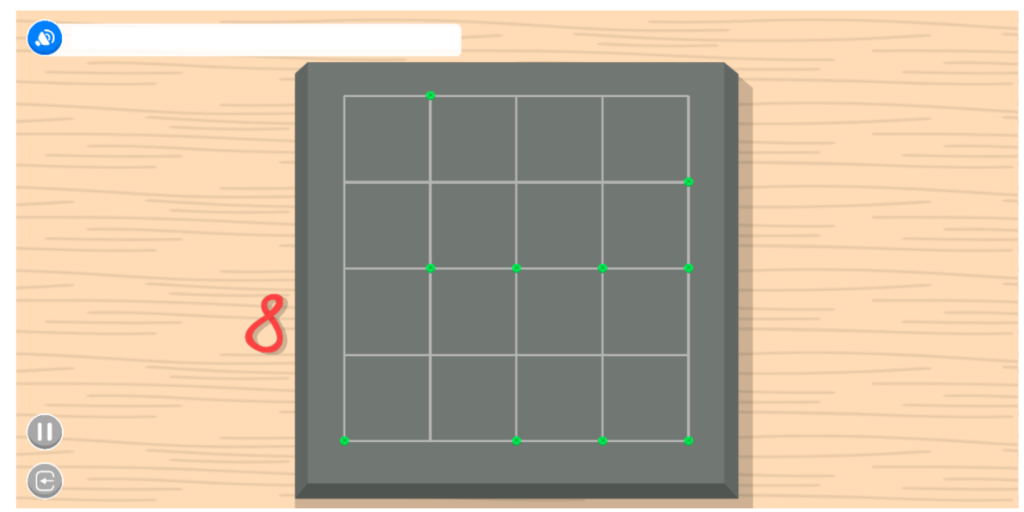
- Poligonoak eraikitzeko 2 zeregin
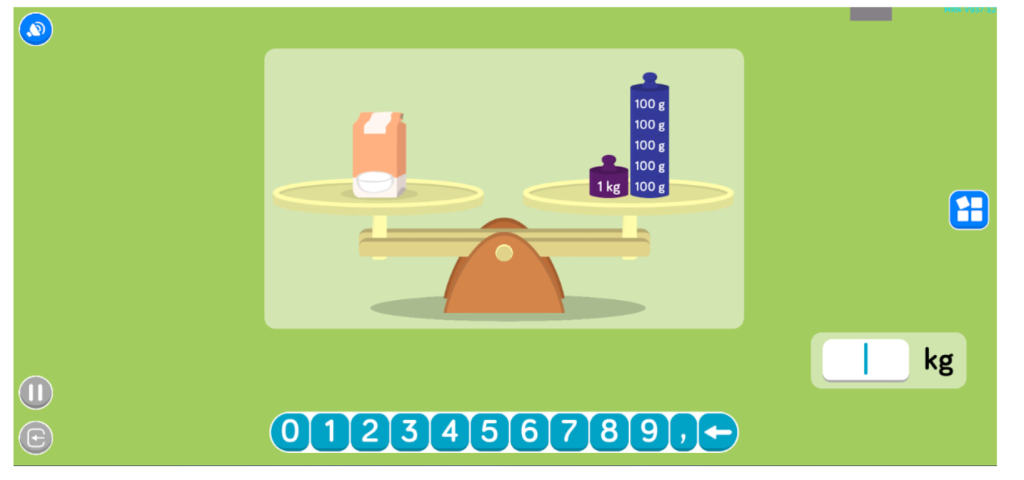
- g-tik kg-ra eta alderantziz pasatzeko 4 zeregin
- 3D gorputzak eraikitzeko 4 zeregin
Ekoizpen-praktika, aplikazioarekin

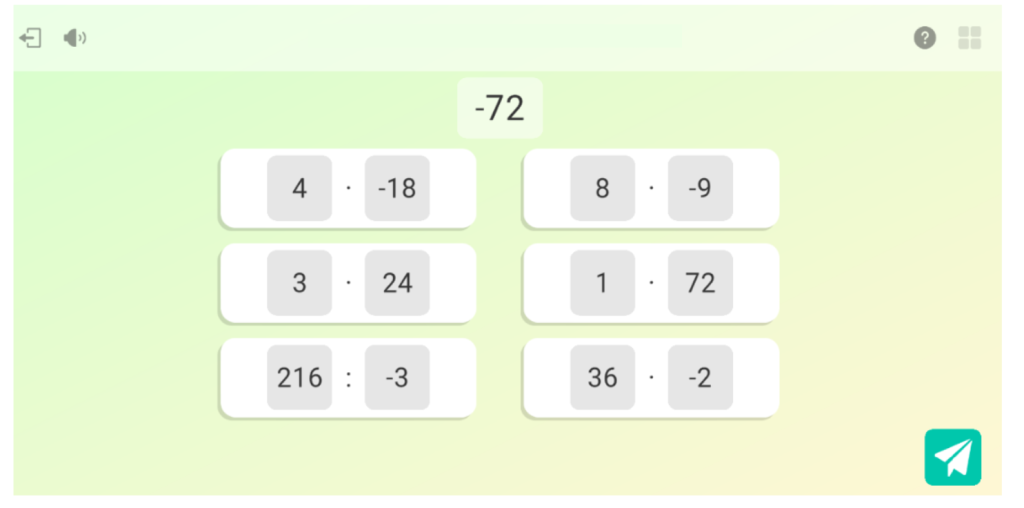
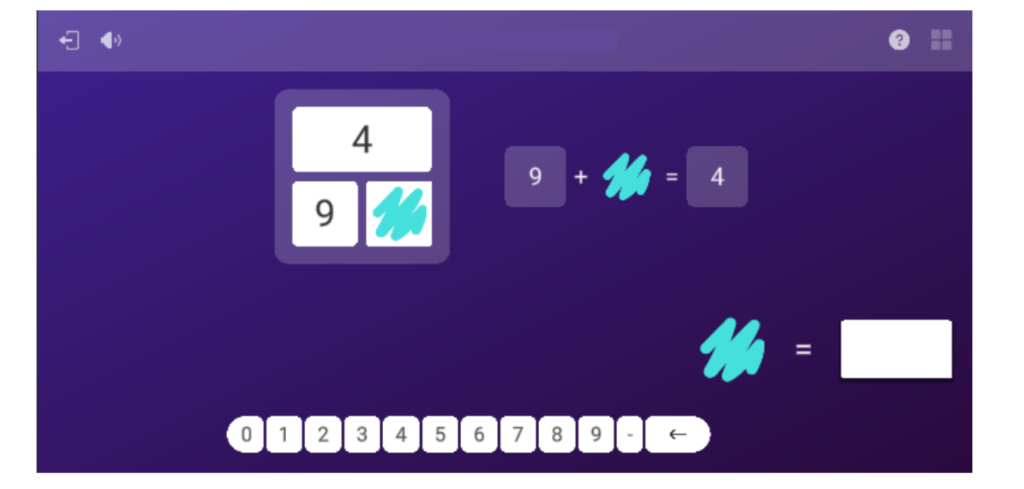
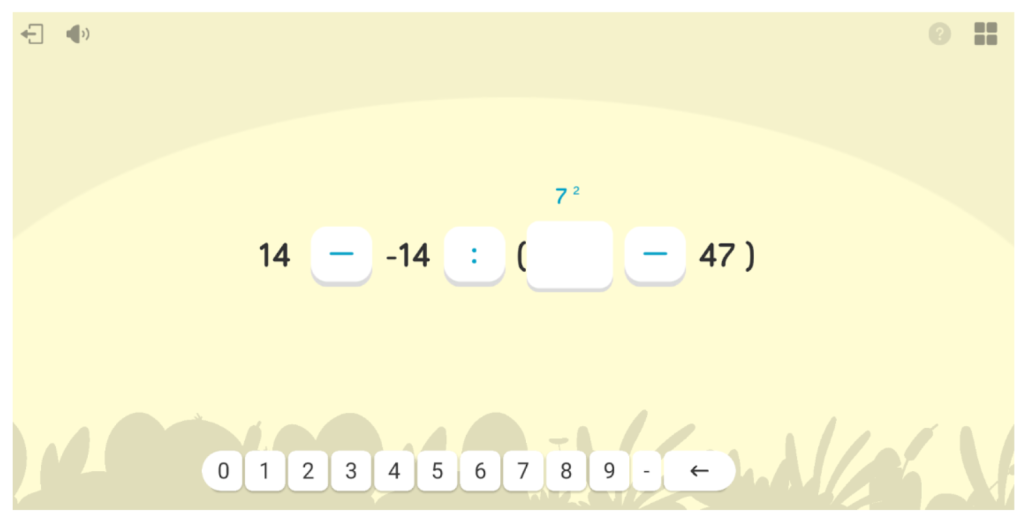

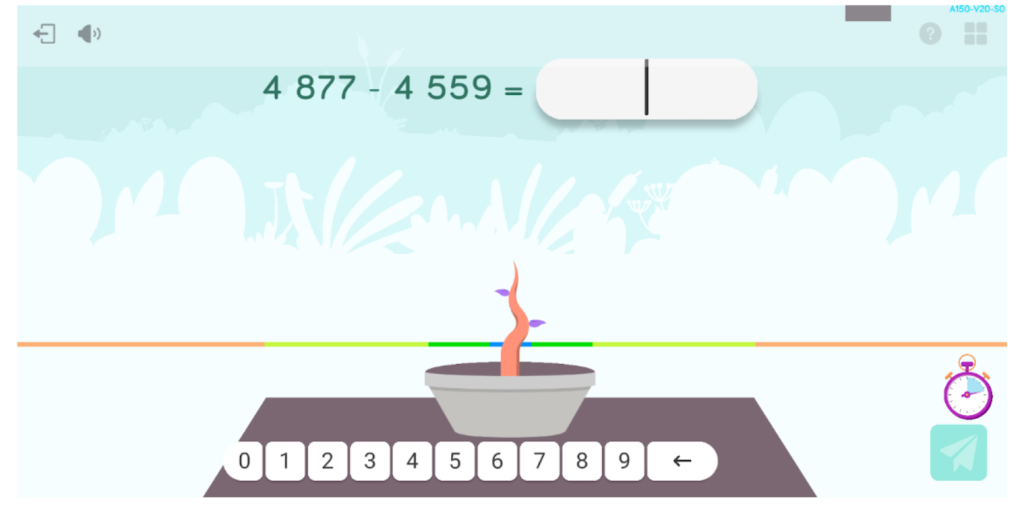



Orokorrean, saioan zehar motibazio-maila altua izan zuen Eduardek, eta ahalegin handia egin zuen jarduerak egitean. Gainera, jarduera bakoitzaren amaieran 0 eta 3 izar artean jaso zituen, asmatu zituen erantzunen eta behar izan zituen laguntza-aholkuen arabera. Guztira, beraz, lor zitzakeen 42 izarretatik 31 izar lortu zituen egun hartan eta, beraz, nahiko pozik egon zitekeen.
Praktika digitalari buruzko artikulu honetan azaltzen dugun moduan, Eduardek bizitako esperientzian bi gauza ikus ditzakegu: batetik, praktika digitalari esker ikasleak adiago eta motibatuago daudela eta feedback-a berehala eta etengabe jasotze dutela, eta, bestetik, irakasleek ez dutela ezer zuzendu beharrik (aste amaieran txosten xehatua jasotzen dute); aldiz, ikasleak beha ditzakete, eta haien beharrei arreta handiagoa eskaini.







