Gran part dels alumnes que mostren un baix rendiment en matemàtiques a l’inici de primària milloren la seva fluïdesa aritmètica si fan una hora a la setmana d’activitats dissenyades per treballar el concepte de nombre. En altres paraules, els estudiants incrementen la seva capacitat per fer operacions i procediments matemàtics simples amb agilitat. Així ho mostra l’estudi ARTIST (Estudi de Resposta a la Intervenció Automatitzada, per les seves sigles en anglès), publicat recentment per la revista acadèmica SN Social Sciences, que ha dut a terme l’equip d’R+D d’Innovamat. L’estudi valida un programa d’intervenció precoç, que consisteix en un test de nivell inicial, una intervenció de suport per als alumnes amb més dificultats, i un segon test posterior. Aquest últim avalua, per una banda, la resposta de cada alumne a la intervenció, i, per l’altra, l’efectivitat de l’eina.
Metodologia de l'estudi
L’estudi ARTIST parteix del marc teòric de la Resposta a la Intervenció (RTI, per les seves sigles en anglès), que consisteix en, primer, detectar aquells alumnes que tenen un baix rendiment i poden necessitar reforç; segon, intervenir en el seu aprenentatge; i tercer, veure com responen a la intervenció. La literatura científica demostra que aquest marc permet desenvolupar eines més eficaces a l’hora d’identificar i abordar el baix rendiment acadèmic que les que parteixen d’altres marcs teòrics1.
L’objectiu d’ARTIST era comprovar si les eines desenvolupades per Innovamat són capaces d’implementar eficaçment el marc teòric RTI. Per dur a terme l’estudi, l’equip d’investigació va seleccionar 13 centres escolars de Catalunya, dels quals 5 van formar part del grup d’intervenció, i 8 del grup control. Els 418 alumnes de primer de primària d’aquests centres van fer un test de cribratge universal, per identificar quins es trobaven en el percentil més baix de fluïdesa aritmètica. Aquest test consta de 8 tasques que avaluen les següents habilitats cognitives i coneixements subjacents a l’aprenentatge de les matemàtiques:

Velocitat d’execució
Clica el talp repetidament tan ràpid com puguis fins que s’acabi el temps.

Velocitat de processament visual
Troba la imatge entre les opcions, o clica NO, si no està.

Coneixement del dígit
Clica el dígit més gran repetidament tan ràpid com puguis fins que s’acabi el temps.

Comparació de magnituds
Observa les imatges de punts durant un breu període de temps i indica de quin color hi ha més punts.

Recta numèrica
Indica en quina posició de la recta es troba el nombre.

Fluïdesa aritmètica
Resol operacions tan ràpid com puguis fins que s’acabi el temps.
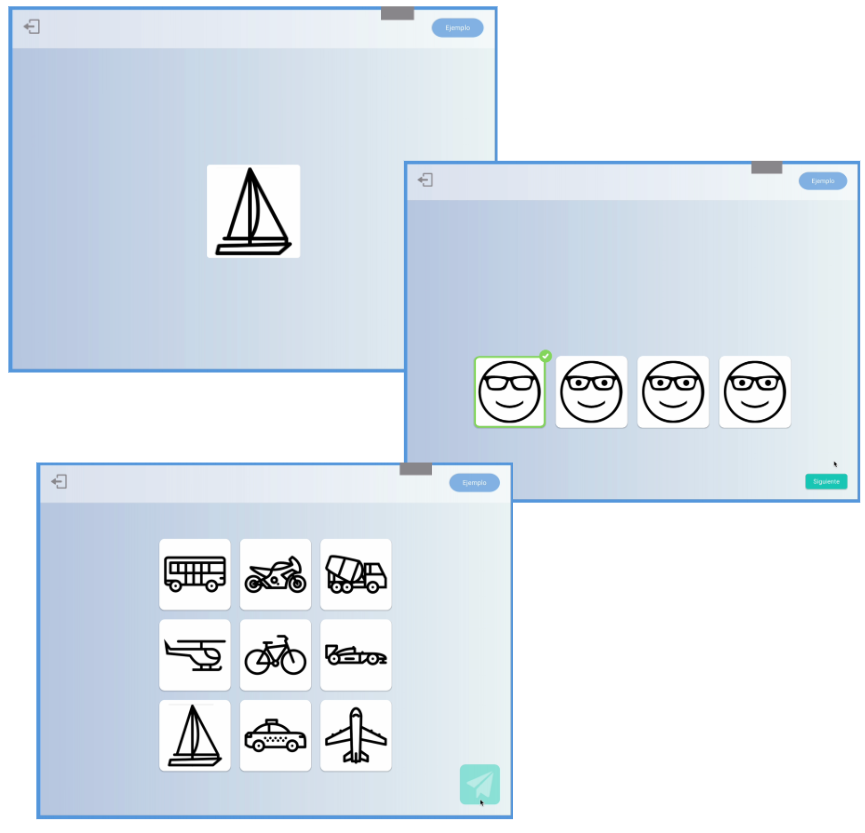
Memòria de treball
Primer memoritza les imatges. A continuació, selecciona la cara diferent de les 4. Al final, selecciona totes les imatges que hagis vist.
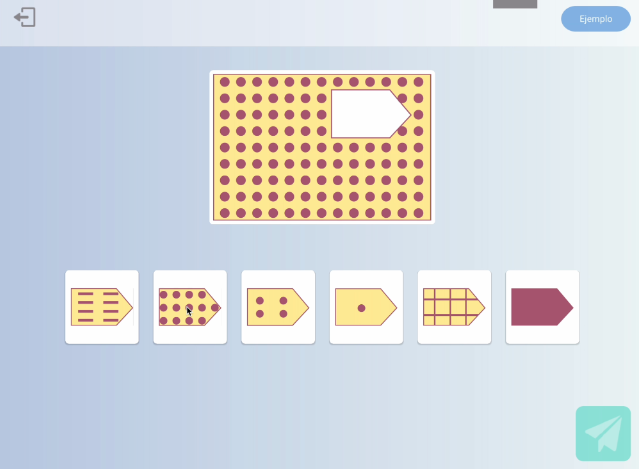
Raonament
Selecciona la peça que completa la imatge.
Figura 1. Activitats del test de cribratge universal, on s’avaluen les habilitats cognitives i coneixements subjacents a l’aprenentatge de les matemàtiques.
Dels 121 alumnes que van mostrar baix rendiment matemàtic en el test, 48 assistien als 5 centres del grup d’intervenció. La intervenció va consistir a oferir a aquests alumnes una sèrie d’activitats fora de l’horari lectiu de matemàtiques per practicar durant 15 minuts al dia, 4 dies a la setmana, i al llarg de 15 setmanes. En finalitzar el programa d’intervenció, els alumnes participants en l’estudi van dur a terme de nou la prova, per analitzar la seva evolució.
Les activitats de la intervenció van ser dissenyades per treballar el concepte de nombre, un concepte bàsic del llenguatge matemàtic que té un impacte positiu en l’aprenentatge d’altres continguts, d’acord amb diversos estudis2. Això significa que, durant la intervenció, no es va entrenar als alumnes per fer sumes com més ràpid millor: la millora del concepte de nombre comporta que, de forma indirecta, millori també la fluïdesa aritmètica.
Com a mostra, a continuació veiem l’exemple d’una activitat basada en un joc inspirat per Butterworth i Laurillard (2016)3. L’activitat desplega una fila de boles que els nens poden separar i unir per produir conjunts amb un nombre determinat d’elements. La tasca consisteix a replicar un nombre objectiu específic. Cada nombre està codificat per colors (2A). A mesura que els alumnes progressen en l’activitat, les xifres aràbigues que identifiquen la quantitat de boles s’incorporen al disseny, la qual cosa fomenta l’associació entre el nombre i la seva representació simbòlica (2B). Una vegada que els alumnes dominen aquesta associació, es retiren les pistes de color perquè la comprensió numèrica no depengui d’això (2C). Posteriorment, també s’amaguen les boles (encara que es poden recuperar fent clic en el dígit) i es deixa només el nombre simbòlic, per progressar cap a l’abstracció (2D). Finalment, s’eliminen completament les boles, que passen a ser una línia numèrica (2E-F). El valor dels nombres objectiu s’amplia progressivament, començant per 2 i fins a 10.
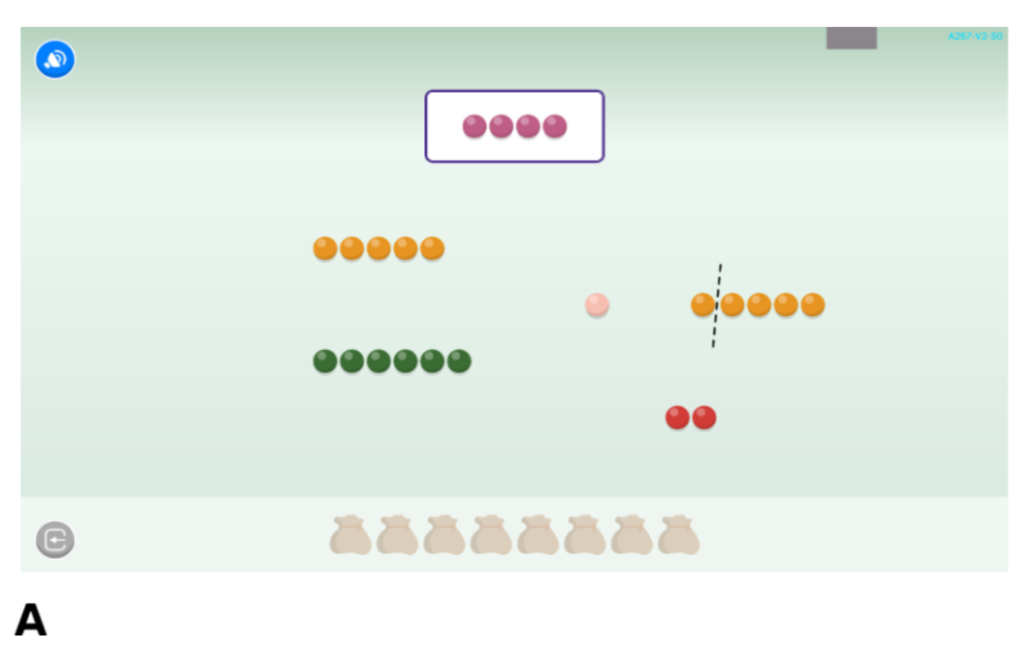
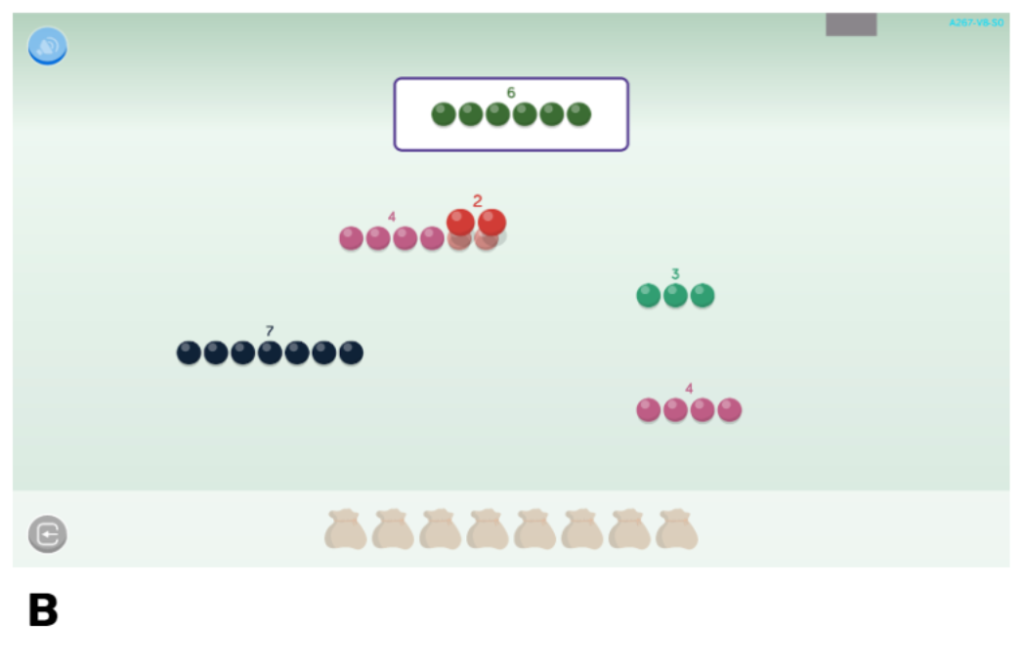

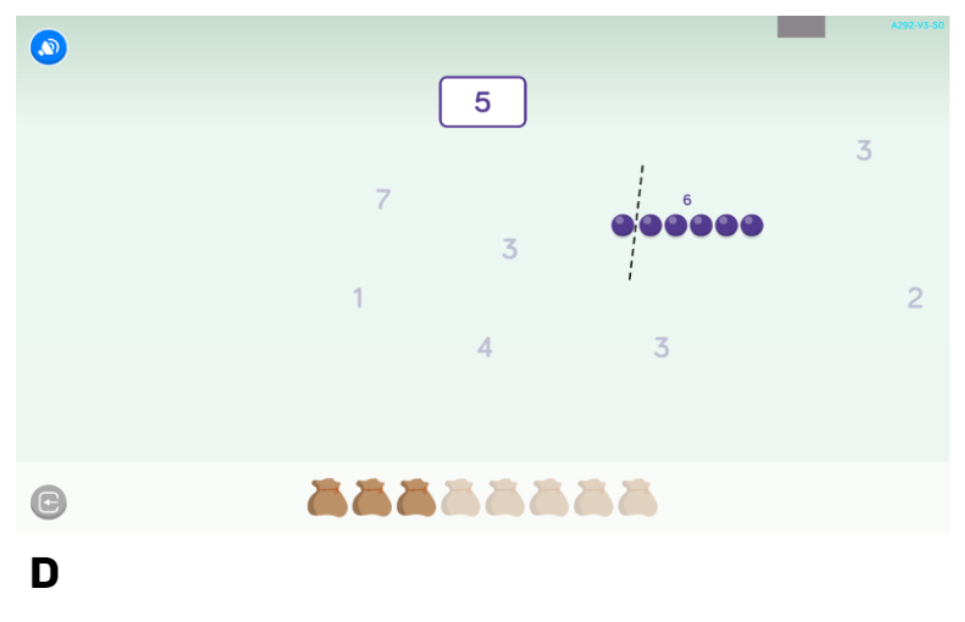

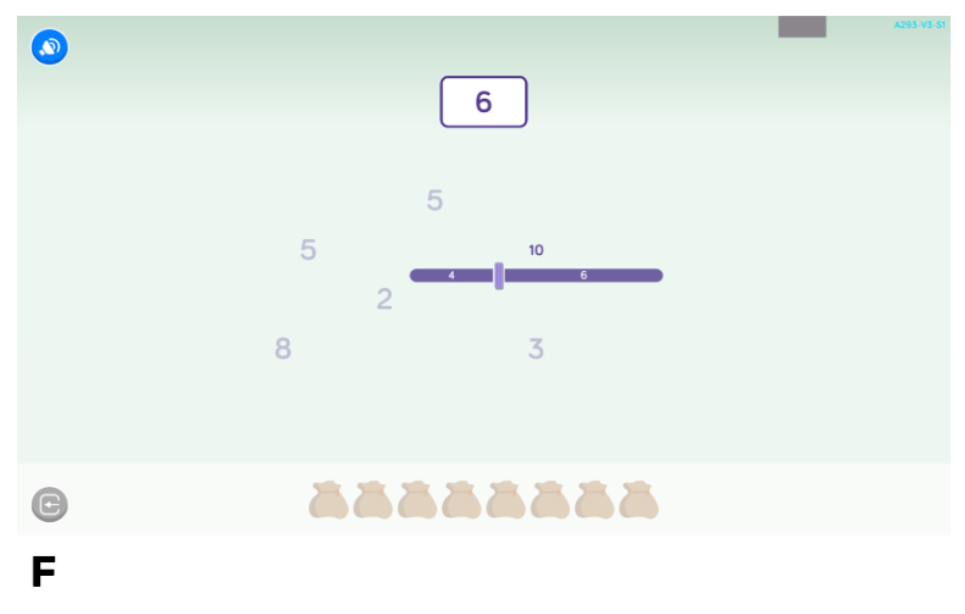
Figura 2. Progressió didàctica de l’activitat d’adquisició del concepte de nombre.
La intervenció primerenca millora la fluïdesa aritmètica
La investigació compara la millora en fluïdesa aritmètica dels alumnes amb un baix rendiment, segons si han participat en la intervenció de suport o no. Els resultats obtinguts mostren que aquells que han format part de la intervenció no només milloren la seva fluïdesa aritmètica significativament més que la resta, sinó que un 81% d’aquests alumnes supera la puntuació que en el test inicial els havia identificat com a alumnes de baix rendiment. Sense cap intervenció, per contra, el percentatge d’alumnes que supera la zona de baix rendiment després del mateix període de temps és del 53%.
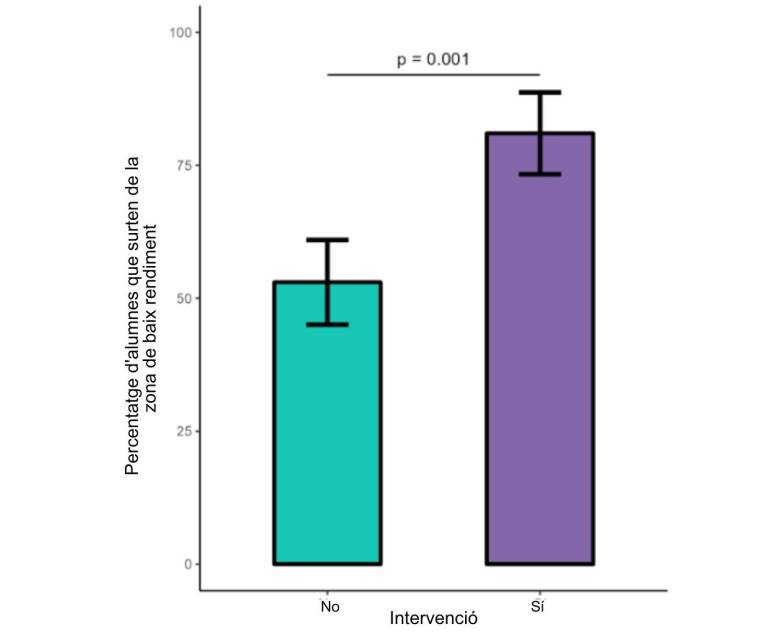
Figura 3. Percentatge d’alumnes que surten de la zona de baix rendiment en el test posterior, segons hagin fet intervenció (dreta, en violeta) o no l’hagin feta (esquerra, en verd). Les barres d’error indiquen l’interval de confiança al 95%. El p-valor = 0.001 prové d’un test de Chi quadrat sobre els resultats.
En resum, els resultats mostren que el percentatge d’alumnes amb baix rendiment que van participar en la intervenció i van millorar, és significativament major que el percentatge d’alumnes que no va rebre intervenció. Òbviament, en el mateix període, els alumnes que no havien estat identificats com a alumnes de baix rendiment també van millorar els seus resultats, però en menor grau.
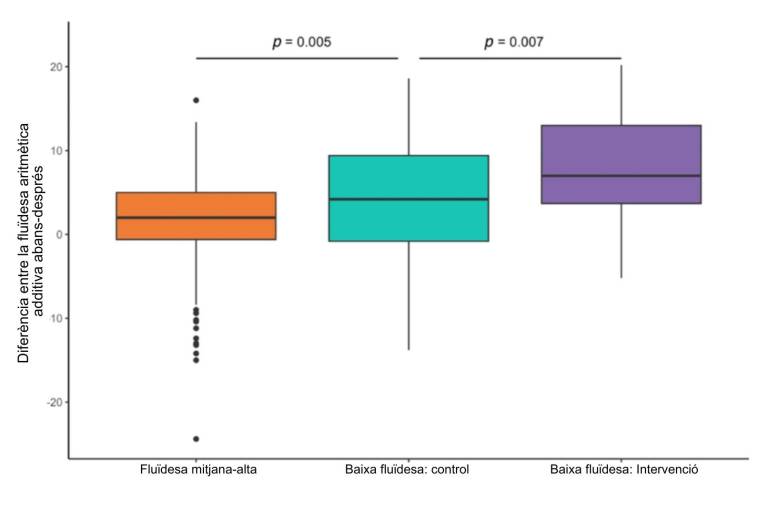
Figura 4. Comparació de les diferències entre la fluïdesa aritmètica additiva abans i després del període d’intervenció: el grup «Fluïdesa mitjana-alta» correspon als alumnes de les 13 escoles que van obtenir una puntuació igual o superior al percentil més baix. Els grups «Baixa fluïdesa: control» i «Baixa fluïdesa: Intervenció» són els de les 8 escoles de control i 5 d’intervenció, respectivament, que van obtenir una puntuació inferior al percentil.
Aquesta millora és fonamental, ja que sabem que les diferències de rendiment entre l’alumnat en els primers cursos escolars tendeixen a accentuar-se al llarg de l’escolarització4. A més, diverses investigacions ens diuen que el sentit numèric i la fluïdesa aritmètica, més que altres factors, prediuen l’èxit matemàtic dels estudiants en el futur. Per això és crucial intervenir com més aviat millor i ajudar aquells alumnes amb dificultats en aquest aspecte5.
Fer accessible la intervenció primerenca als centres educatius
Un dels objectius de l’estudi també ha estat desenvolupar eines escalables que permetin implementar RTI en sistemes educatius que no estan familiaritzats amb aquest marc teòric o no disposin de recursos humans per desplegar-lo. Per donar resposta a aquesta problemàtica, l’equip d’R+D d’Innovamat ha optat per una solució tecnològica que fa més accessibles aquests recursos.
No és necessari utilitzar la tecnologia per implementar RTI, però aquesta permet portar-la a les aules sense que suposi un important sobreesforç tant econòmic com humà per als centres. L’estudi ARTIST mostra que és possible implementar el marc RTI amb èxit en sistemes educatius que no tenen recursos dedicats expressament a aquest fi. Actualment, 43 centres educatius s’han sumat a la implementació d’aquest programa d’intervenció.
Els resultats d’aquest estudi mostren que la investigació té un impacte real en la trajectòria educativa de l’alumnat. És clau continuar acostant la investigació a l’aula a través d’eines validades científicament que ens ajudin a millorar l’aprenentatge de les matemàtiques del nostre alumnat.
Referències
1
Fletcher JM, Vaughn S (2009) Response to intervention: preventing and remediating academic difficulties. Child Develop Perspect 3(1):30–37. https://doi.org/10.1111/j.1750-8606.2008.00072.x
Hughes CA, Dexter DD (2011) Response to intervention: a research-based summary. Theory Pract 50(1):4–11. https://doi.org/10.1080/00405841.2011.534909
Gersten R, Haymond K, Newman-Gonchar R, Dimino J, Jayanthi M (2020) Meta-analysis of the impact of reading interventions for students in the primary grades. J Res Educ Eff 13:1–27. https://doi.org/10.1080/19345747.2019.1689591
2
Butterworth, B. (2018). Dyscalculia: From science to education. Routledge.
3
Butterworth B, Laurillard D (2016) Investigating dyscalculia: a science of learning perspective. In: From the laboratory to the classroom. Routledge, pp 184–202. https://doi.org/10.1126/science.1201536
4
Duncan, G. J., Dowsett, C. J., Claessens, A., Magnuson, K., Huston, A. C., Klebanov, P., Pagani, L., Feinstein, L., Engel, M., Brooks-Gunn, J., Sexton, H., Duckworth, K., Japel, C., Cordray, D., Ginsburg, H., Grissmer, D., Lipsey, M., Raver, C., Sameroff, A., … Zill, N. (2006). School Readiness and Later Achievement.
Geary DC (2011) Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Dev Psychol 47(6):1539–1552. https://doi.org/10.1037/a0025510
5
Geary DC (2011) Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Dev Psychol 47(6):1539–1552. https://doi.org/10.1037/a0025510
Jordan et al (2009) Early math matters: kindergarten number competence and later mathematics outcomes. Dev Psychol 45(3):850–867. https://doi.org/10.1037/a0014939
Vasilyeva M, Laski EV, Shen C (2015) Computational fluency and strategy choice predict individual and cross-national differences in complex arithmetic. Dev Psychol 51(10):1489–1500. https://doi.org/10.1037/dev0000045








