Tabla de contenidos
La regla de tres es un concepto matemático que abordamos en diferentes cursos de primaria. El algoritmo de la regla de tres se ha convertido en una herramienta muy recurrente para resolver problemas relacionados con la proporcionalidad. Sin embargo, ¿es realmente necesario saber el algoritmo para tener nociones de proporcionalidad? ¿Podríamos presentar la regla de tres desde diferentes puntos de vista? En este artículo ejemplificamos cómo un aprendizaje aparentemente mecánico puede ser competencial.
¿Qué es la regla de tres?
En nuestro día a día, a menudo, nos encontramos con situaciones que podemos analizar matemáticamente gracias a la proporcionalidad: compramos a granel, una cantidad u otra de un mismo producto; modificamos una receta de cocina para un número diferente de comensales; puede ser que dividamos una tarea entre los miembros de un grupo y luego cambie el número de miembros; calculamos descuentos en las rebajas; convertimos unidades de medida, etc.
Estas son situaciones que tradicionalmente resolvíamos con la regla de tres. A continuación exponemos algunos ejemplos resueltos mediante dicho procedimiento.
4 botellas de agua cuestan 2,30 €. ¿Cuánto pagaremos si queremos comprar 10 botellas?

6 operarios realizan un trabajo en 10 horas. ¿Cuánto tardarán en realizar el mismo trabajo 15 operarios?

En una tienda de la calle Mayor están de rebajas. En la puerta hay un cartel que dice: «20 % de descuento en pantalones». ¿Cuánto cuestan ahora unos pantalones que antes costaban 45 €?

En Estados Unidos, las alturas se miden en pies (en inglés, feet, que se abrevia ft). Sabemos que 3 m son, aproximadamente, 10 ft. ¿Cuánto mide, en metros, un árbol de 6,5 ft?
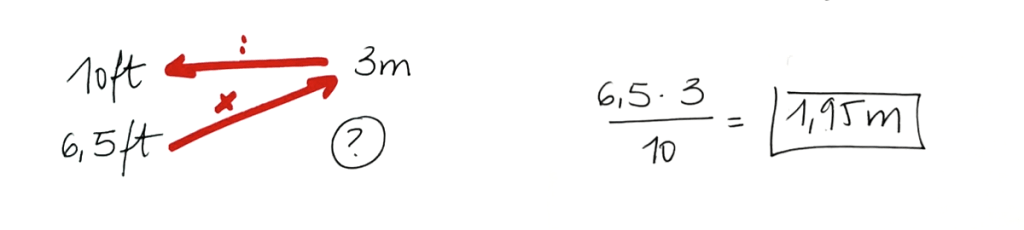
Este tipo de resolución algorítmica requiere de habilidad memorística. La regla de tres es un algoritmo que permite conocer el dato oculto a partir de colocar los datos conocidos de una manera concreta para realizar unas operaciones aritméticas en un orden determinado. Como en cualquier algoritmo cerrado, ni la posición que ocupan los números, ni las operaciones se pueden alterar, pues no obtendríamos el resultado correcto. Sabemos que presentar algoritmos de forma prematura a nuestros alumnos provoca cierta pasividad en su pensamiento. No razonan, y cuando los pasos del algoritmo fallan, se bloquean, por lo que si presentamos el algoritmo demasiado pronto, provocamos que les cueste desarrollar herramientas para continuar frente a una dificultad.
Imaginad el siguiente ejemplo:
Si 10 músicos tocan la Novena sinfonía de Beethoven en 65 min, ¿cuánto tardarán 5 músicos?
Los alumnos que estén acostumbrados a aplicar la regla de tres sin pensar pueden caer en la trampa y equivocarse. Con los algoritmos tradicionales, al ser poco transparentes, no es fácil hacer conexiones con contenidos matemáticos que ayudan a entender el porqué de las operaciones que se realizan.
En las siguientes líneas analizaremos situaciones diferentes de proporcionalidad, tanto directa como inversa, y otras que tienen que ver con el cálculo de porcentajes o el cambio de unidades. Tradicionalmente, los porcentajes y los cambios de unidades se resolvían mediante algoritmos propios, pero en realidad comparten la idea de proporcionalidad y, en consecuencia, la regla de tres puede dar respuesta con más o menos eficiencia a la situación. ¡Veamos las conexiones!
Regla de tres vs. tablas de proporcionalidad
En Innovamat defendemos que la introducción de los algoritmos debe darse cuando estemos seguros de que el alumno, aunque olvidara los pasos, tendría recursos suficientes para resolver la situación. En nuestras secuencias didácticas los algoritmos se construyen, no se dan.
No creemos que la regla de tres deba desaparecer de la clase de matemáticas, pero estamos convencidos de que el aprendizaje debe ser competencial, es decir, debe surgir de la comprensión. En lugar de decir «voy a resolver esta situación con una regla de tres», diremos: «voy a resolver esta situación por proporcionalidad».
Utilizar un algoritmo con el único fin de ganar eficacia es insuficiente, este no puede ser el único motivo para presentar un recurso al alumnado. Con este tipo de prácticas, corremos el riesgo de dar una visión distorsionada de lo que significa hacer matemáticas. La actividad matemática no consiste en hacer grandes cuentas o solo seguir algoritmos, sino que implica pensar, buscar patrones y relaciones entre datos.
Por otro lado, la principal dificultad de los alumnos frente a la regla de tres es que no son capaces de recordar el orden de las operaciones o la posición de las magnitudes en el papel. Si los alumnos no han llegado a la regla de tres acompañados y mediante otros algoritmos más transparentes, a menudo no saben qué están haciendo y convierten la regla de tres en una estrategia carente de sentido, en un ejercicio únicamente memorístico.
Además, introducirla demasiado pronto en primaria entorpece el trabajo sobre la relación multiplicativa entre números y esconde algunas relaciones no aditivas entre números. A su vez, en secundaria puede impedirnos profundizar en las ideas de razón y proporción.
Como alternativa a la regla de tres, defendemos la resolución de estas situaciones a través de una profunda comprensión de la proporcionalidad, mediante el razonamiento lógico, la reducción a la unidad y el cálculo mental. Las tablas de proporcionalidad sí son un recurso eficaz para construir con los alumnos.
A continuación, retomamos los ejemplos anteriores y ponemos el foco en las ventajas de utilizar las tablas de proporcionalidad para resolverlos.
4 botellas de agua cuestan 2,30 €. ¿Cuánto pagaremos si queremos comprar 10 botellas?

Una estrategia que los alumnos aplican fácilmente es reducir a la unidad la magnitud independiente. Al pasar por la unidad se dan cuenta de que pueden encontrar el precio de cualquier cantidad de botellas de ese tipo. Aquí podemos trabajar la idea de razón de proporcionalidad. Por cada botella, pagaremos 0,575 € (resultado de dividir 2,30 € entre 4).
Por otro lado, si observamos que 10 botellas son «dos veces y media» el paquete de 4, también lo será el precio que paguemos por ellas.
6 operarios realizan un trabajo en 10 horas. ¿Cuánto tardarán en realizar el mismo trabajo 15 operarios?
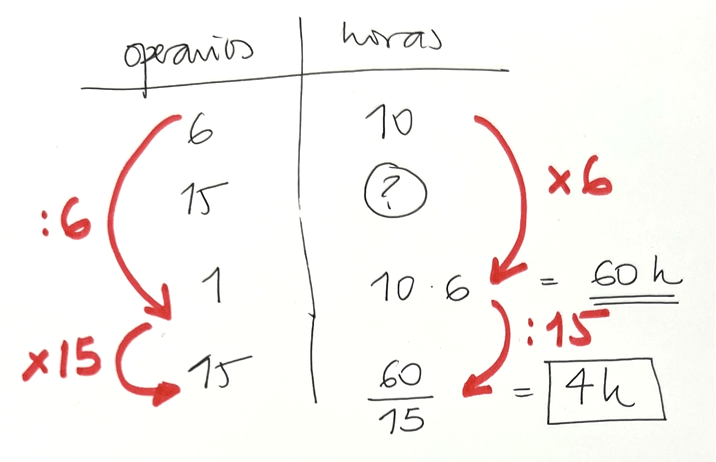
Este tipo de resolución evita el error común de no saber cuáles son y en qué orden se realizan las operaciones de multiplicación y división en la regla de tres inversa.
En esta situación, los alumnos comprenden y aplican con naturalidad que, cuantos más operarios trabajen, menos tiempo necesitarán para acabar el trabajo.
En una tienda de la calle Mayor están de rebajas. En la puerta hay un cartel que dice: «20 % de descuento en pantalones». ¿Cuánto cuestan ahora unos pantalones que antes costaban 45 €?

Este tipo de tablas nos ayudan a comprender la naturaleza de los porcentajes entendidos como una fracción de denominador 100 (un 20 % es lo mismo que ⅕ de una unidad).
En este caso también damos mucha importancia a que el alumno vea que un 20 % de descuento es equivalente a pagar el 80 % del precio; lo que evita tener que realizar la resta final y obtener el resultado directamente.
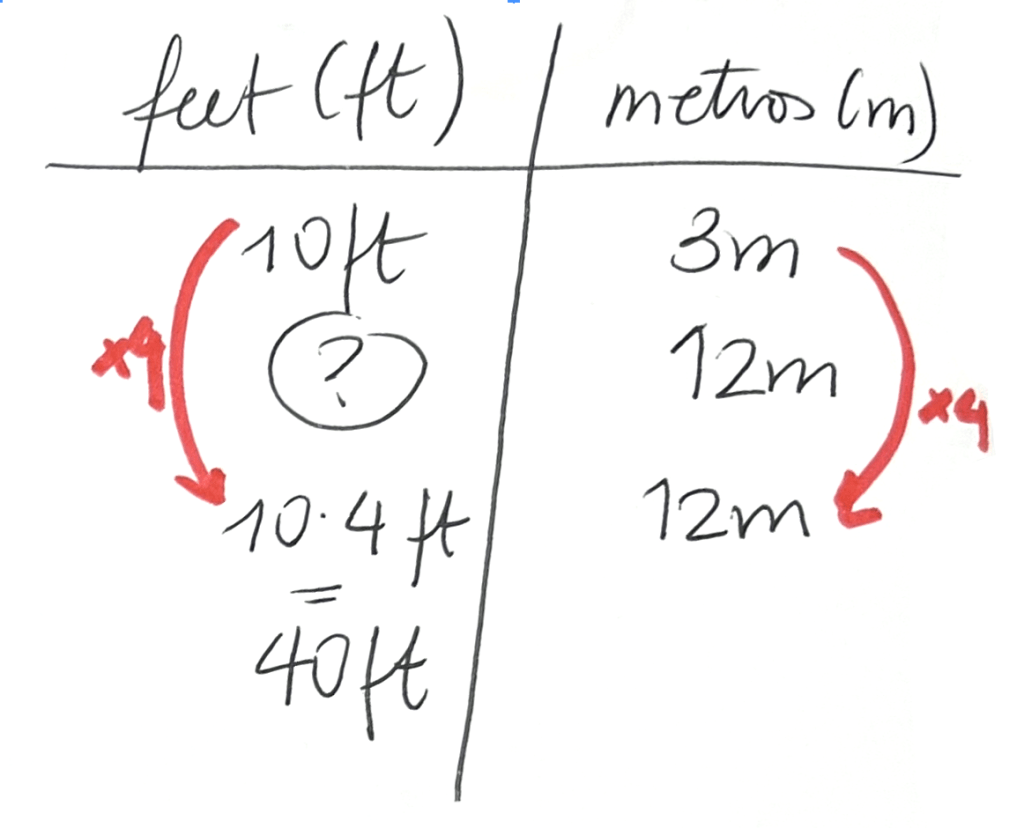
En Estados Unidos, las alturas se miden en pies (en inglés, feet, que se abrevia ft). Sabemos que 3 m son, aproximadamente, 10 ft. ¿Cuánto mide, en metros, un árbol de 6,5 ft?

Aquí, los alumnos conocen la equivalencia (10 pies es lo mismo que 3 metros), por lo que pueden medir en pies y dar la respuesta en metros, como en el enunciado. Y también podrían medir en metros y dar la respuesta en pies, como proponemos a continuación.
Reflexionemos sobre el aprendizaje de las matemáticas
A modo de conclusión nos gustaría insistir en la idea de que la regla de tres puede convertirse en una muleta ficticia para los alumnos, ya que no promueve el desarrollo de su competencia matemática. Al depender exclusivamente de la aplicación mecánica de la fórmula, se limita su comprensión conceptual y su capacidad para resolver problemas de manera autónoma. Es necesario replantear la enseñanza de la regla de tres y buscar enfoques más integrales que fomenten la comprensión, el razonamiento y la autonomía en las matemáticas. Por eso, hablar de dominar la proporcionalidad podría ser positivo para no tener una visión distorsionada de las matemáticas y verlas como lo que son: una manera de vivir, ver y entender el mundo.






