¿Es necesario saber las tablas de multiplicar de memoria? ¿Hay que fomentar el esfuerzo en matemáticas? ¿Y la práctica, es importante?
Estas son algunas de las preguntas que nos hacéis llegar a menudo; y no hemos querido perder la oportunidad de convertirlas en un juego.
¿Te apuntas?
1/5 ¿Ha cambiado la manera de hacer las operaciones básicas?
Hacemos las operaciones de la misma manera; lo que cambia es cómo las aprendemos.
Para que el alumnado tenga fluidez en la resolución de operaciones y llegue al resultado correcto de manera eficiente, es necesario construir fomentando una comprensión profunda: ¿qué estamos haciendo y por qué funciona?
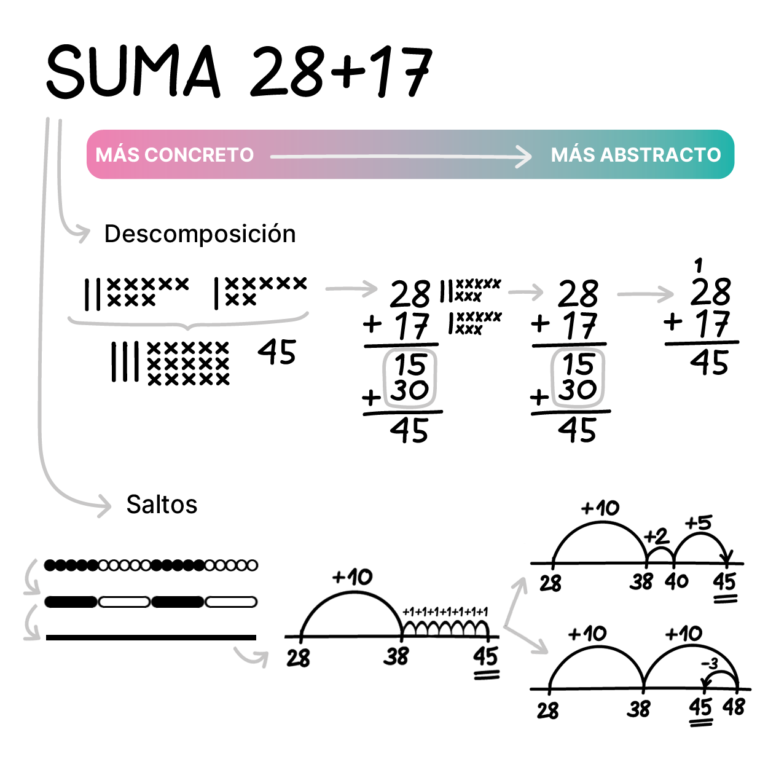
Para construir con significado las operaciones básicas (suma, resta, multiplicación y división), se presentan diferentes estrategias. El dominio de las distintas estrategias, además de aumentar la comprensión, favorece la flexibilidad en los cálculos.
Cada una de estas estrategias tiene un proceso de aprendizaje diseñado para maximizar esta comprensión. Comenzamos por lo más concreto, utilizando materiales manipulativos, hasta llegar a lo más abstracto, consiguiendo una representación más eficiente y compacta.
- Van Den Heuvel-Panhuizen, M. (2008). Children Learn Mathematics: A Learning-Teaching Trajectory with Intermediate Attainment Targets for Calculation with Whole Numbers in Primary School. Dutch Design in Mathematics Education, Vol. 1. Utrecht: Freudenthal Institute, Sense Publishers.
-
Kilpatrick, J., Swafford, J., Findell, B., & National Research Council (U.S.), Mathematics Learning Study Committee. (2001). Adding it up: Helping children learn mathematics. National Academy Press.
2/5 ¿Es importante practicar?
La práctica es esencial para consolidar los conocimientos y ganar fluidez.
Por eso, es importante dedicar momentos a la práctica reproductiva: enfocada a lograr el dominio de un procedimiento concreto mediante su repetición. Y también momentos a la práctica productiva, donde la práctica se convierte en una excusa para poner en juego los procesos matemáticos, como la resolución de problemas.
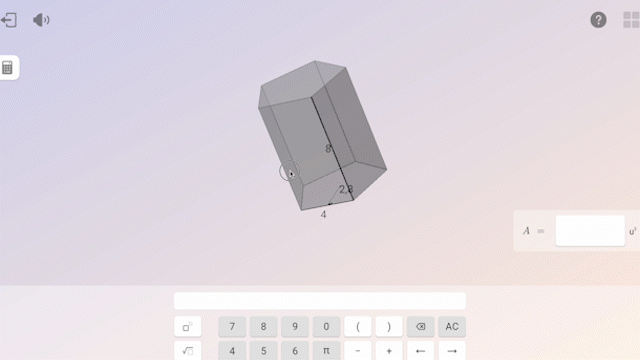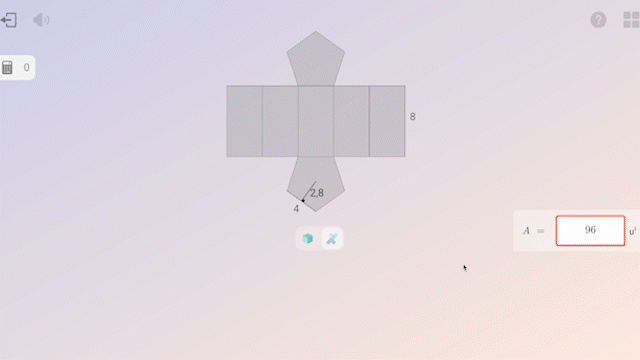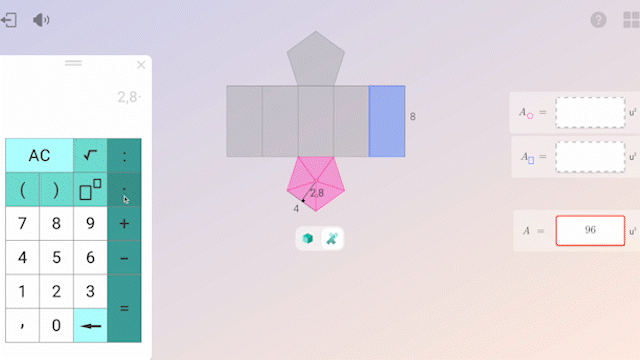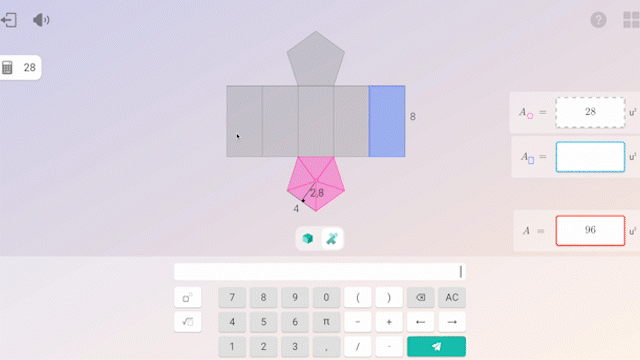
El uso de la tecnología en la práctica aporta un valor añadido: permite individualizar el aprendizaje, ofreciendo retorno inmediato e informes detallados sobre el progreso de cada alumno. Esto permite a los docentes ajustar el acompañamiento a cada estudiante.

- Spangler, D. A., & Wanko, J. J. (2017). Enhancing Classroom Practice with Research Behind Principles to Actions. NCTM.
-
Pettersson, F. (2017). On the issues of digital competence in educational contexts – a review of literature. Education and Information Technologies, 23(3), 1005–1021. https://doi.org/10.1007/s10639-017-9649-3
3/5 ¿Las tablas de multiplicar deben acabar sabiéndose de memoria?

La automatización de las tablas es imprescindible para lograr aprendizajes significativos en conceptos posteriores, como las divisiones o las potencias.
Después de construir las tablas de multiplicar, es el momento de practicarlas para que el alumnado automatice los resultados y desarrolle estrategias para deducir rápidamente aquellos que aún no se sabe de memoria.
No saberse las tablas aumenta la carga cognitiva en problemas avanzados, ya que los alumnos deben dedicar esfuerzo a cálculos básicos, reduciendo su capacidad para concentrarse en aspectos más complejos.
-
Bay-Williams, J. M., & SanGiovanni, J. J. (2022). Accessing Fluency through Routine and Opportunity. NCTM Annual Meeting 2022. Los Angeles.
-
Vilalta, A., Calvo, C., & Correig, E. (2023). Automatizar las tablas de multiplicar: un propósito que va más allá de 3.º EP. UNO: Revista de Didáctica de las Matemáticas, 99, 61-67.
-
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257-285.
4/5 ¿Deben plantearse unas matemáticas que se aprendan sin esfuerzo?

El esfuerzo en el aprendizaje de las matemáticas no debe evitarse, sino aprovecharlo para aprender. Hablamos de esfuerzo productivo (del inglés productive struggle), que consiste en desarrollar perseverancia y flexibilidad de pensamiento, en lugar de simplemente buscar la solución correcta.
Los docentes ajustamos este esfuerzo planteando retos adecuados, sin dar respuestas directas, y fomentando la motivación y la autonomía de los alumnos.
Tener una mentalidad de crecimiento es fundamental para ver los errores como oportunidades para avanzar en el proceso de aprendizaje, desarrollando resiliencia y manteniendo la motivación.
- Boaler, J. (2016). Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages, and Innovative Teaching. Jossey-Bass.
-
Dweck, C. S. (2006). Mindset: The New Psychology of Success. Random House.
5/5 ¿Nosotros, como docentes, tenemos un papel relevante en todo esto?

Ningún recurso o material, por muy bien diseñado que esté, puede tener éxito sin la dedicación y experiencia de los docentes.
No hay fórmulas mágicas: vuestro compromiso, formación continua y confianza en el potencial de los alumnos son los verdaderos motores de su aprendizaje.
Por ello, las guías didácticas y las oportunidades de formación son herramientas valiosas que podéis aprovechar para seguir creciendo como profesionales y ofrecer la mejor experiencia posible a vuestros alumnos.
-
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22.
-
Darling-Hammond, L. (2000). Teacher quality and student achievement: A review of state policy evidence. Education Policy Analysis Archives, 8(1), 1-44.
Si os ha despertado curiosidad, os animamos a consultar nuestro libro blanco, donde exploramos a fondo estas y otras cuestiones.
Estamos aquí para apoyaros y trabajar juntos para impulsar el aprendizaje matemático del alumnado.
¡Hasta pronto!






