Descarga el nuevo Ebook
Descubre este recurso que sintetiza de manera visual algunas de las estrategias más utilizadas de las operaciones básicas.

Artículos relacionados:
La suma (próximamente)
La resta (próximamente)
La multiplicación (próximamente)
La división (próximamente)
Sabemos que las matemáticas no son solo operaciones, pero ¿qué es más importante para el aprendizaje de esta parte fundamental de las matemáticas: entender lo que hacemos, llegar al resultado correcto o resolver las operaciones en un tiempo razonable?
Como docentes, las expectativas en el aprendizaje de nuestros alumnos deben ser altas. ¡Así que debemos ser ambiciosos!
Los alumnos deben entender qué hacen y por qué lo hacen.
Tienen que llegar al resultado correcto aplicando los procedimientos correctamente.
Y también deben resolver las operaciones de forma eficiente y en un tiempo razonable.
Como veis, la respuesta no es excluyente: los tres objetivos son indispensables. Ahora bien, somos conscientes de que es un objetivo ambicioso. Sobre todo cuando gestionamos el aula de un grupo de alumnos que apenas emprenden el camino en las matemáticas.
Así pues, en este artículo exploramos cómo abordar el aprendizaje de las matemáticas para lograr fluidez.
¿Entender antes de aplicar o aplicar antes de entender?
Peter Liljedahl, en el libro Diseñando aulas para pensar en matemáticas, propone 14 prácticas para fomentar la participación de los alumnos y conseguir que piensen. Estas prácticas están orientadas a crear aulas donde los estudiantes sean los verdaderos protagonistas, invitándolos a ir más allá de la simple repetición mecánica.
¿Por qué deberíamos fomentar aulas donde los alumnos solo ejecuten mecánicamente lo que podría hacer mejor y más rápidamente una máquina? En cambio, cuando un alumno entiende conceptos como qué significa restar o por qué utilizamos determinadas estrategias, como los saltos sobre la línea numérica, obtiene una base más sólida para los nuevos aprendizajes.
Ahora bien, poner el foco en la comprensión no significa que no tengan que resolver correctamente las operaciones. Sí que deben llegar al resultado correcto. Por eso en el aula también se dedica tiempo a la práctica para consolidar los aprendizajes y ganar fluidez.

Dentro de este contexto, el papel del maestro como guía es indispensable. El docente debe ayudar a descubrir las estrategias de manera clara y transparente. Y, después, asegurarse de que los alumnos siguen consolidando los contenidos a través de la práctica, animándolos a salir de su zona de confort e incrementando paulatinamente la dificultad de los retos y procedimientos.
Por ejemplo, cuando un alumno ha resuelto correctamente algunas restas (dependiendo de cada alumno) utilizando material manipulativo, es momento de invitarlo a trabajar sin ese material, pero utilizando representaciones visuales. Después, cuando haya resuelto correctamente algunas operaciones más con este nuevo enfoque, debemos retirar de nuevo estos andamiajes y acompañarlo a realizar un cambio de representación cada vez más abstracto. Y así sucesivamente.
Estos apoyos, o andamiajes, son esenciales en las primeras fases del aprendizaje. Pero deben desaparecer gradualmente para que el alumno alcance un pensamiento más abstracto y vaya ganando fluidez. El objetivo es completar el recorrido hasta que pueda resolver las operaciones sin ningún tipo de apoyo. Pero, eso sí, teniendo estrategias a las que recurrir en caso de que lo necesite.
Construcción de estrategias basada en el modelo CRA
Cada una de las estrategias sigue una secuencia de aprendizaje concreta basada en la comprensión: qué estamos haciendo.
Por eso, seguimos el modelo CRA (concreto, representativo, abstracto), una metodología de aprendizaje matemático basada en tres etapas progresivas que ayudan a los alumnos a comprender y dominar los conceptos matemáticos.
Primero, partimos de la manipulación con diferentes materiales (concreto); a continuación, representamos en papel lo que hacíamos manipulativamente (representativo), y, finalmente, pasamos a las representaciones abstractas, como los algoritmos (abstracto).
¿Qué entendemos por fluidez?
La investigación define la fluidez como la habilidad de trabajar con números, operaciones y procedimientos con soltura.
La fluidez tiene tres niveles de profundidad:
Fluidez factual (fact fluency): habilidad para evocar hechos conocidos o derivados con soltura gracias a la automatización. Dentro de este marco entra la automatización de sumas de un dígito, en 1º y 2º de primaria (7 + 3 = 10; 6 + 4 = 10; 8 + 7 = 15), y la automatización de las multiplicaciones de un dígito (tablas de multiplicar), en 3º y 4º de primaria.
Fluidez computacional (computational fluency): habilidad para realizar operaciones (computar), con soltura, más allá de las operaciones simples. Dentro de este marco entran habilidades tan clave que van desde ejecutar correctamente la estrategia de saltos hasta el modelo de repartos de la división.
Fluidez procedimental (procedural fluency): habilidad para seguir con soltura procedimientos que van más allá de una operación básica y que dependen de cada etapa. Aquí nos referimos a encontrar el mcm, resolver operaciones combinadas, resolver ecuaciones, etc.
Además, dentro de la definición de fluidez, existen tres componentes clave y seis acciones relacionadas:
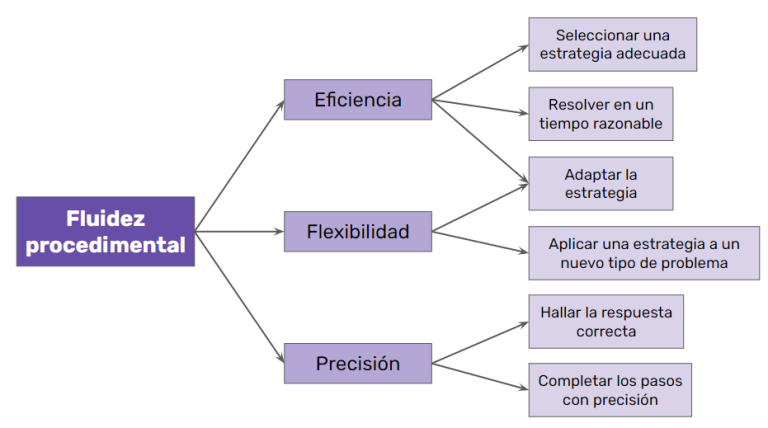
Como veis, tener fluidez no es solo resolver operaciones rápidamente. También implica ser eficiente y flexible a la hora de elegir una estrategia, adaptarla según el contexto y llegar al resultado correcto, completando los pasos con precisión.
¿Qué hechos se deben saber responder con rapidez?
A menudo, cuando hablamos de un aprendizaje basado en la comprensión profunda de los conocimientos, parece que demonizamos completamente la velocidad en la respuesta, pero existen distintos contenidos que deberían formar parte del conocimiento automático de los alumnos. Son:
La automatización de sumas de un dígito (rango 0-10)
La automatización de las multiplicaciones de un dígito (tablas de multiplicar)
De hecho, son algunos de los contenidos que entran dentro del marco de la fluidez factual. El no saber responder rápidamente y, todavía más, no tener estrategias eficientes para deducir los resultados, comporta que los alumnos tengan que dedicar esfuerzos a cálculos básicos, lo que reduce la capacidad de concentrarse en aspectos más avanzados o complejos.
Por eso es importante saber responder deprisa, ya sea porque nos lo sabemos de memoria o porque lo hemos deducido muy rápidamente a partir de unos cuantos resultados básicos sin mucho esfuerzo. Por ejemplo, un alumno puede deducir muy rápidamente que 60 + 70 = 130 de 6 + 7 = 13.
Cómo conseguir eficiencia y flexibilidad a partir de la construcción de diversas estrategias
Como hemos visto, uno de los pilares para desarrollar fluidez es conocer diferentes formas de enfrentar las operaciones. Es decir, dominar diversas estrategias que nos permitan resolver cualquier operación dependiendo del contexto y de los números implicados. En definitiva, tener flexibilidad.
Fijémonos en las sumas y restas, por ejemplo. A veces, conviene utilizar el algoritmo escrito. Otras veces, preferimos hacer un cálculo mental imaginando saltos sobre la línea numérica. También hay momentos en los que podemos deducir el resultado a partir de hechos que ya conocemos. Incluso hay ocasiones en las que queremos utilizar la calculadora.
Conocer esta variedad, y saber elegir, es lo que nos hace ser flexibles y eficientes al calcular. Sin embargo, la práctica es la que nos ayudará a ganar agilidad en la ejecución.
El aprendizaje significativo de las operaciones básicas
El aprendizaje de las matemáticas (sobre todo la parte de numeración) tiene una estructura jerárquica: es necesario pisar un contenido para poder avanzar hacia el siguiente. Las operaciones básicas (suma, resta, multiplicación y división) son fundamentales en este proceso, ya que allanan el terreno para sembrar otros conceptos más avanzados de numeración y/o álgebra.
Más allá de los algoritmos, dominar cada operación básica implica entender su significado, saber cómo se resuelve y qué estrategias podemos utilizar para conseguirlo.
Cada operación es como un iceberg: lo que vemos en la superficie es solo una pequeña parte de toda la complejidad. Todo lo que se mantiene bajo el agua es lo que sostiene y da sentido al dominio de cada operación.
Así pues, hemos ideado este recurso. Un librito que resume de forma sintética y visual todo lo que esconde el aprendizaje de cada operación básica:
- Qué significa sumar, restar, multiplicar y dividir.
- Qué estrategias se proponen para resolver cada operación.
- Qué secuencia de aprendizaje, basada en el modelo CRA, sigue cada estrategia.
Tener este conocimiento nos permitirá ser más flexibles y eficientes. Aun así, practicar será esencial para ganar rapidez en los cálculos, un aspecto que trabajaremos más adelante.
De momento, te invitamos a sumergirte en este recurso y a explorar sus profundidades para convertir el aprendizaje de cada operación en una oportunidad para pensar, entender y progresar.
Descarga el nuevo Ebook
Descubre este recurso que sintetiza de manera visual algunas de las estrategias más utilizadas de las operaciones básicas.

Referencias bibliográficas:
Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22-31.
Bay-Williams, J. M., y SanGiovanni, J. J. (2021). Figuring out fluency: Mathematics teaching and learning, grades K-8: Moving beyond basic facts and memorization (1st ed.). Corwin.
Hmelo‐Silver, C. E., Duncan, R. G., y Chinn, C. A. (2007). Scaffolding achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 99–107. https://doi.org/10.1080/0046150701263368
Van den Heuvel-Panhuizen, M. (2008). Children learn mathematics: Learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Dutch design in mathematics education, V: 1. Utrecht: Freudenthal Institute, Sense Publishers.







