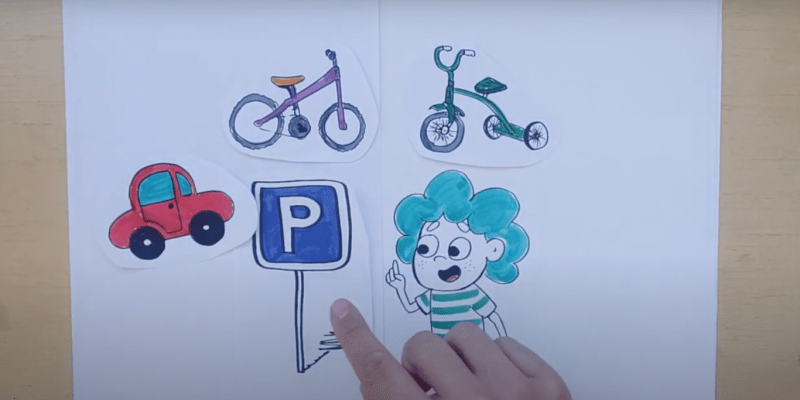Si queréis saber qué son y cómo proponemos gestionar estas tareas, podéis consultar este enlace.
Contenidos más relevantes: Numeración y cálculo, combinatoria, números, sumas, multiplicaciones, tablas de multiplicar.
Idea original: https://nrich.maths.org/136
I. ¡Planteemos y empecemos a pensar!
https://youtu.be/N3JEG1zFXUg?list=PLhV04eMTllAo5NYwNeoBBquwFsRSWBtLf
¿Cuántos vehículos hay en el parking?
Pretendemos que el alumnado comprenda que la solución a la pregunta depende de qué vehículos haya, y que representen diversas soluciones. Para encontrarlas todas, el alumnado deberá seguir alguna estrategia ordenada que les permita argumentarlo justificadamente.
II. ¡Comprobemos y sigamos pensando!
https://youtu.be/6KuVKyDJ3B8?list=PLhV04eMTllAo5NYwNeoBBquwFsRSWBtLf
¿Y si Paula hubiera contado 15 ruedas?
Pretendemos que el alumnado compruebe si han encontrado todas las soluciones y que reflexionen sobre la manera de representarlas. Había 7 maneras diferentes de sumar 12 ruedas:
- 3 coches
- 2 coches y 2 bicis
- 1 coche y 4 bicis
- 1 coche, 2 triciclos y 1 bici
- 6 bicis
- 3 bicis y 2 triciclos
- 4 triciclos
Además, el alumnado deberá razonar para descubrir cómo cambia la solución si son 15 ruedas en vez de 12. Si conviene, también podemos hacer otras preguntas como: Y si sabemos que en el parking no hay triciclos, ¿qué pasaría?
Y si sabemos que en el parking no hay triciclos, ¿qué pasaría?
III. ¡Reflexionemos y vayamos más allá!
https://youtu.be/OqULLuKbOHg?list=PLhV04eMTllAo5NYwNeoBBquwFsRSWBtLf
Pretendemos que el alumnado reflexione sobre las nuevas soluciones y que compruebe si las han encontrado todas. Además, esperamos que incorporen los aprendizajes sobre la eficiencia en la representación de la tarea anterior en esta nueva cuestión. Había la misma cantidad de soluciones, 7:
- 5 triciclos
- 3 triciclos y 3 bicicletas
- 3 triciclos, 1 bicicleta y 1 coche
- 1 triciclo y 6 bicicletas
- 1 triciclo, 4 bicicletas y 1 coche
- 1 triciclo, 2 bicicletas y 2 coches
- 1 triciclo y 3 coches
Por otro lado, la respuesta a la pregunta alternativa propuesta es:
Y si sabemos que en el parking no hay triciclos, ¿qué pasaría?
Que las cantidades de ruedas deberían ser pares. En otras palabras, si la cantidad de ruedas es impar, por fuerza tiene que haber triciclos.
¡No hay ningún cambio en el número de soluciones entre 12 y 15 ruedas! ¿Y si fueran 13 ruedas? Con 13 ruedas hay menos soluciones, solo 5:
- 3 triciclos y 1 coche
- 3 triciclos y 2 bicicletas
- 1 triciclo y 5 bicicletas
- 1 triciclo, 3 bicicletas y 1 coche
- 1 triciclo, 1 bicicleta y 2 coches
De hecho, cualquier cantidad de ruedas a partir de 2 tiene solución. Y solo si Paula dijera que ha contado 2, 3 o 5 ruedas sería solución única.