Si voleu saber què són i com proposem gestionar aquestes tasques, podeu consultar aquest enllaç.
Continguts més rellevants: Numeració i càlcul, nombres, sumes, restes, regularitats.
Idea original: http://www.cut-the-knot.org/Curriculum/Games/ProizvolovGame.shtml
I. Plantegem i comencem a pensar!
Què heu descobert?
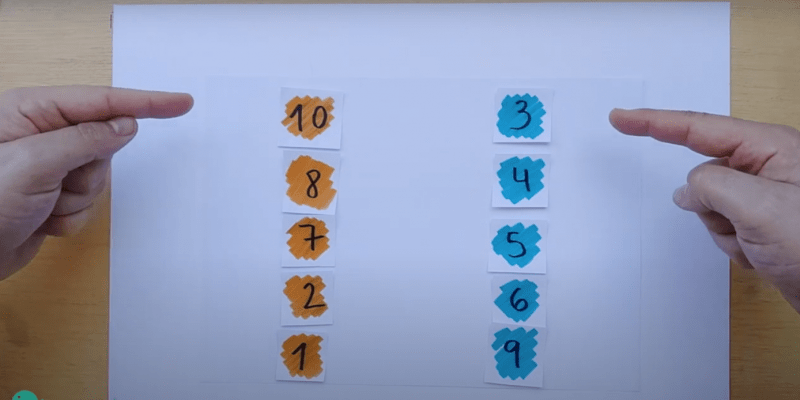
Pretenem que els infants facin diverses proves i investiguin els resultats mentre ordenen, resten i sumen, a la recerca de patrons.
II. Comprovem i seguim pensant!
I amb els nombres de l’1 al 12, què observeu?
Pretenem que els infants, després de fer diverses proves, analitzar, comparar i raonar, s’adonin com a mínim de la regularitat en el resultat de la suma, que sempre és 25. No pretenem que descobreixin per què ni que ho justifiquin, tot i que pot ser interessant de veure amb alguns infants. Sempre dóna 25 perquè, independentment de l’ordre en què posem els nombres, la suma final sempre és:
10 + 9 + 8 + 7 + 6 – 5 – 4 – 3 – 2 – 1 =
= (10 – 3) + (8 – 4) + (7 – 5) + (6 – 2) + (9 – 1) =
= (10 – 5) + (9 – 4) + (8 – 3) + (7 – 2) + (6 – 1) =
= 5 + 5 + 5 + 5 + 5 = 5 x 5 = 25
A més, els infants hauran de raonar per descobrir com afecta el canvi en les condicions de l’enunciat a les solucions que havia trobat fins ara. Al vídeo, proposem què passarà amb els nombres de l’1 al 12, però es poden triar altres rangs.
III. Reflexionem i anem més enllà!
Pretenem que els infants descobreixin que tot i canviar el rang de l’1 al 12, la suma també es manté constant. Aquesta vegada, sempre dóna 36 perquè, independentment de l’ordre en què posem els nombres, la suma final sempre és:
12 + 11 + 10 + 9 + 8 + 7 – 6 – 5 – 4 – 3 – 2 – 1 = 6 x 6 = 36
I amb altres rangs? Per exemple, si agafem nombres entre 1 i 2n, sempre dona n2. O si agafem nombres entre x i x + 2n – 1 també, sempre dóna n2. Per últim, és interessant fer reflexionar els infants que, per tal que el problema es pugui resoldre, la quantitat de nombres ha de ser parell. Per exemple, al vídeo es proposa de fer entre 3 i 11 però, com que això són 9 nombres, no es pot. Si els infants ens ho fan notar, llavors els podem demanar com canviarien l’enunciat per poder-ho fer (afegint o traient un nombre), i que ho intentin.