Taula de continguts
La regla de tres és un concepte matemàtic que abordem en diferents cursos de primària. L’algoritme de la regla de tres s’ha convertit en una eina molt habitual per resoldre problemes relacionats amb la proporcionalitat. Ara bé, realment cal saber l’algoritme per tenir nocions de proporcionalitat? Podríem presentar la regla de tres des de diferents punts de vista? En aquest article exemplifiquem com un aprenentatge aparentment mecànic pot ser competencial.
Què és la regla de tres?
En el nostre dia a dia, sovint ens trobem amb situacions que podem analitzar matemàticament gràcies a la proporcionalitat: comprem a granel una quantitat o una altra d’un mateix producte; modifiquem una recepta de cuina per a un nombre diferent de comensals; dividim una tasca entre els membres d’un grup i després canvia el nombre de membres; calculem descomptes a les rebaixes; convertim unitats de mesura, etc.
Aquestes situacions tradicionalment les resolíem amb la regla de tres. A continuació mostrem alguns exemples resolts mitjançant aquest procediment.
4 ampolles d’aigua costen 2,30 €. Quant pagarem si volem comprar 10 ampolles?
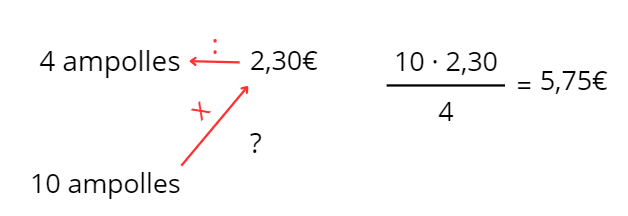
6 operaris fan una feina en 10 hores. Quant trigaran a fer la mateixa feina 15 operaris?
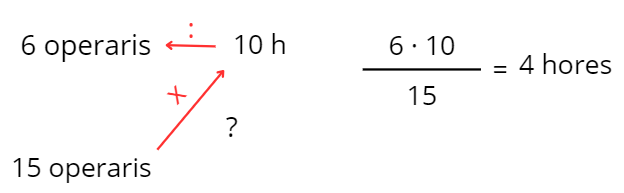
En una botiga del carrer Major estan de rebaixes. A la porta hi ha un cartell que diu: «20 % de descompte en pantalons». Quant costen ara uns pantalons que abans costaven 45 €?

Als Estats Units, les alçàries es mesuren en peus (en anglès, feet, que s’abreuja ft). Sabem que 3 m són, aproximadament, 10 ft. Quant mesura, en metres, un arbre de 6,5 ft?
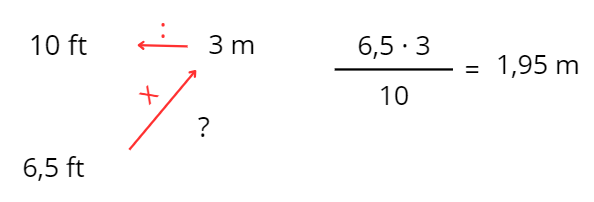
Aquesta mena de resolució algorítmica requereix habilitat memorística. La regla de tres és un algoritme que permet conèixer la dada que falta a partir de col·locar les dades conegudes d’una manera concreta i fer unes operacions aritmètiques en un ordre determinat. Com en qualsevol algoritme tancat, ni la posició que ocupen els nombres, ni les operacions que fem es poden alterar, ja que, si no, no obtindríem el resultat correcte. Sabem que presentar algoritmes de forma prematura als nostres alumnes els provoca una certa passivitat en el pensament. No raonen, i quan els passos de l’algoritme fallen, es bloquegen. Si presentem l’algoritme massa aviat, doncs, provoquem que els costi desenvolupar eines per continuar davant d’una dificultat.
Imagineu l’exemple següent:
Si 10 músics toquen la Novena simfonia de Beethoven en 65 min, quant trigaran 5 músics?
Els alumnes que estiguin acostumats a aplicar la regla de tres sense pensar poden caure a la trampa i equivocar-se. Amb els algoritmes tradicionals, com que són poc transparents, no és fàcil establir connexions amb continguts matemàtics que ajudin a entendre el perquè de les operacions que es fan.
En l’apartat següent analitzarem diverses situacions de proporcionalitat, tant directa com inversa, i d’altres que tenen a veure amb el càlcul de percentatges o el canvi d’unitats. Tradicionalment, els percentatges i els canvis d’unitats es resolien mitjançant algoritmes propis, però com que comparteixen la idea de proporcionalitat, la regla de tres també pot donar resposta a la situació, amb més o menys eficiència. Vegem-ne les connexions!
Regla de tres vs. taules de proporcionalitat
A Innovamat defensem que la introducció dels algoritmes s’ha de fer quan estiguem segurs que l’alumne, encara que n’oblidés els passos, tindria recursos suficients per resoldre la situació. A les nostres seqüències didàctiques els algoritmes es construeixen, no es donen.
No creiem que la regla de tres hagi de desaparèixer de la classe de matemàtiques, però estem convençuts que l’aprenentatge ha de ser competencial, és a dir, ha de sorgir de la comprensió. En lloc de dir «resoldré aquesta situació amb una regla de tres», direm: «resoldré aquesta situació per proporcionalitat».
Utilitzar un algoritme amb l’únic objectiu de guanyar eficàcia és insuficient, no pot ser l’únic motiu per presentar un recurs als alumnes. Amb aquesta mena de pràctiques, correm el risc de donar una visió distorsionada del que vol dir fer matemàtiques. L’activitat matemàtica no consisteix a fer grans comptes o només seguir algoritmes, sinó que implica pensar, cercar patrons i relacions entre dades.
D’altra banda, la principal dificultat dels alumnes davant de la regla de tres és que no són capaços de recordar l’ordre de les operacions o la posició de les magnituds al paper. Si els alumnes no han arribat a la regla de tres acompanyats i mitjançant altres algoritmes més transparents, sovint no saben què estan fent i converteixen la regla de tres en una estratègia sense sentit, en un exercici únicament memorístic.
A més, introduir-la massa aviat a primària entorpeix el treball sobre la relació multiplicativa entre nombres i amaga algunes relacions no additives entre nombres. Alhora, a secundària ens pot impedir aprofundir en les idees de raó i proporció.
Com a alternativa a la regla de tres, defensem la resolució d’aquestes situacions a través d’una comprensió profunda de la proporcionalitat, mitjançant el raonament lògic, la reducció a la unitat i el càlcul mental. Les taules de proporcionalitat sí que són un recurs eficaç per construir amb els alumnes.
A continuació, reprenem els exemples anteriors i posem el focus en els avantatges de fer servir les taules de proporcionalitat per resoldre’ls.
4 ampolles d’aigua costen 2,30 €. Quant pagarem si volem comprar 10 ampolles?
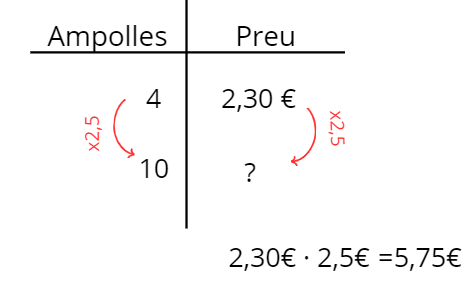
Un raonament que els alumnes apliquen fàcilment és reduir a la unitat la magnitud independent. Quan passen per la unitat s’adonen que poden trobar el preu de qualsevol quantitat d’ampolles del mateix tipus. Aquí podem treballar la idea de raó de proporcionalitat. Per cada ampolla pagarem 0,575 € (resultat de dividir 2,30 € entre 4).
D’altra banda, si observem que 10 ampolles són «dues vegades i mitja» el paquet de 4, també ho ha de ser el preu que en paguem.
6 operaris fan una feina en 10 hores. Quant trigaran a fer la mateixa feina 15 operaris?
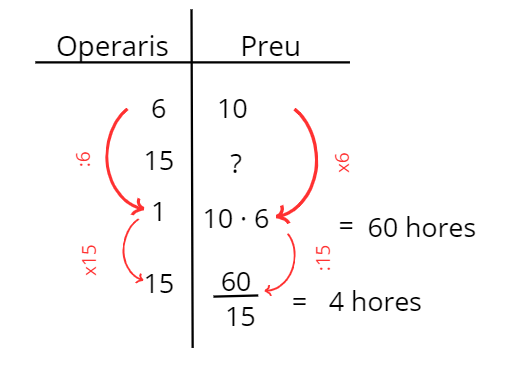
Aquesta mena de resolució evita l’error comú de no saber quines són i en quin ordre es resolen les operacions de multiplicació i divisió a la regla de tres inversa.
En aquesta situació, els alumnes comprenen i apliquen amb naturalitat que, com més operaris treballin, menys temps necessitaran per acabar la feina.
En una botiga del carrer Major estan de rebaixes. A la porta hi ha un cartell que diu: «20 % de descompte en pantalons». Quant costen ara uns pantalons que abans costaven 45 €?
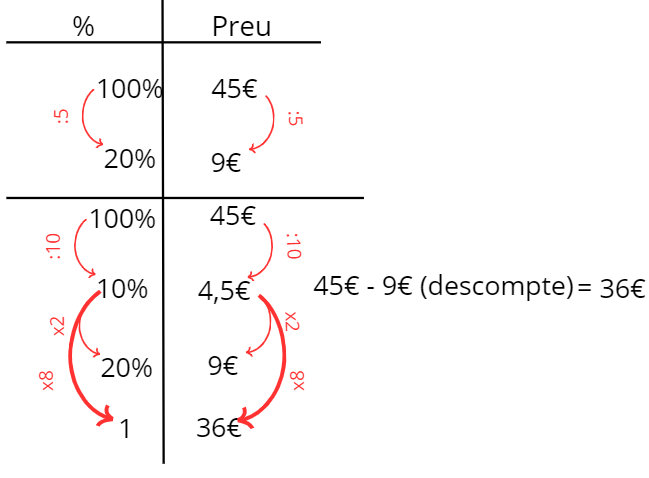
Aquesta mena de taules ens ajuden a comprendre la naturalesa dels percentatges, entesos com a fracció de denominador 100 (un 20 % és el mateix que ⅕ d’una unitat).
En aquest cas també donem molta importància al fet que l’infant vegi que un 20 % de descompte és equivalent a pagar el 80 % del preu; així evitem haver de fer la resta final i obtenim el resultat directament.
Als Estats Units, les alçàries es mesuren en peus (en anglès, feet, que s’abreuja ft). Sabem que 3 m són, aproximadament, 10 ft. Quant mesura, en metres, un arbre de 6,5 ft?
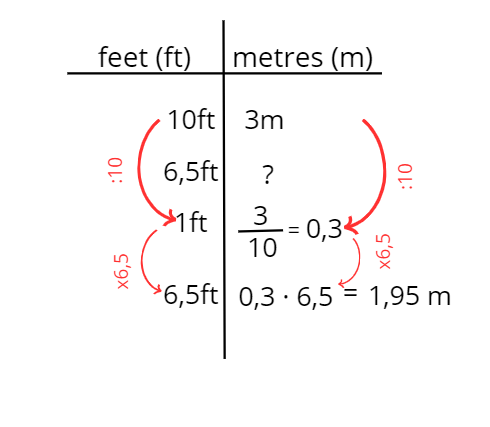
Aquí, els alumnes saben l’equivalència (10 peus és el mateix que 3 metres), de manera que poden fer els càlculs en peus i expressar la resposta en metres, com demana l’enunciat. I també podrien fer els càlculs en metres i donar la resposta en peus, com proposem a continuació.

Reflexionem sobre l'aprenentatge de les matemàtiques
A tall de conclusió ens agradaria insistir en la idea que la regla de tres es pot convertir en una crossa fictícia per als alumnes, ja que no promou el desenvolupament de la competència matemàtica. El fet de dependre exclusivament de l’aplicació mecànica de la fórmula limita la comprensió conceptual i la capacitat per resoldre problemes de manera autònoma. Cal replantejar l’ensenyament de la regla de tres i buscar enfocaments més integrals que fomentin la comprensió, el raonament i l’autonomia en les matemàtiques. Per això, parlar de dominar la proporcionalitat podria ser positiu per no tenir una visió distorsionada de les matemàtiques i veure-les com el que són: una manera de viure, veure i entendre el món.






