Taula de continguts
Com es construeix el concepte de nombre?
L’aprenentatge dels nombres, a l’educació infantil, dura més i és més complex del que sovint imaginem. Construir un concepte de nombre sòlid, resistent als canvis i disponible per ser aplicat a situacions reals diverses inclou un seguit d’aprenentatges parcials, de naturaleses diferents, que cal integrar en un tot. (Piaget, 1952; Kamii, 1983; Canals, 1989)
D’entrada, cada nombre natural correspon a una quantitat, i en cada llengua o cultura tenim una paraula que el designa i un signe (grafia) que l’identifica. Per tant, són tres continguts diferents que cal treballar per separat, però també de manera conjunta, perquè conformen un primer bloc amb moltes interrelacions.

Per exemple, donada una quantitat petita, cal saber reconèixer quants n’hi ha; saber les paraules que designen els números per ordre i també saltejats; saber llegir les xifres i construir-ne la quantitat, etc. tot això són continguts, principalment socials i culturals, necessaris per comprendre i comunicar-nos en relació amb el concepte de nombre. De fet, són eines importants per raonar matemàticament sobre el concepte de nombre, entendre la seva estructura i les seves relacions.
El segon bloc de contingut relatiu a la construcció del concepte de nombre es focalitza en la comparació de quantitats en si mateixes, més enllà de la paraula o del signe que les designa. És a dir, en el fet de comprendre i usar els nombres atenent a les dues relacions que l’integren: la d’equivalència i la d’ordre. Quan parlem de relacions d’equivalència, parlem de saber reconèixer que dos grups formats per objectes amb mides i volum molt diferents (per exemple, 5 caramels i 5 infants) estan formats per la mateixa quantitat malgrat que perceptivament no tinguin res a veure. Aquesta és una fita important. Quan parlem de relacions d’ordre, volem dir saber comparar dos grups fins i tot amb objectes de naturalesa diferent (per exemple, 10 bales i 5 pilotes de futbol) i concloure que, malgrat que la percepció ens diu que en 5 pilotes hi ha més massa, més volum, hi ha més bales que pilotes.
A continuació, vegem dues situacions d’aula on els infants han d’aplicar relacions d’equivalència (tants com…) i d’ordre (més que…, menys que…).

La comprensió de la relació d’ordre dels nombres obre la porta a un nou aprenentatge que cal anar treballant: la inclusió jeràrquica, és a dir, el fet que cada nombre inclou tots els que són més petits que ell.

Per si tot això fos poc, també és necessari aprendre a comptar de manera que aquesta habilitat sigui funcional i ajudi a resoldre situacions quotidianes. L’aprenentatge d’aquesta habilitat inclou: saber la seqüència de paraules que designen els nombres per ordre, establir connexions per tenir la relació ocular-manual-verbal coordinada, saber separar els elements comptats dels que falten (sense repetir-ne cap, ni deixar-se’n) i, finalment, saber que la darrera paraula número que s’ha dit en comptar determina el cardinal de tota la col·lecció. Déu n’hi do! (Schaeffer, Eggleston i Scott, 1974; Dickson, Brown i Gibson, 1991)
I encara no hem acabat! De fet, encara no hem entrat al bloc de conceptes més fonamental per a la construcció sòlida de la idea de nombre: el càlcul. Entenem el càlcul, en aquesta etapa, com les transformacions de les quantitats i l’estudi de la construcció d’aquestes. Efectivament, saber que una quantitat es transforma si li afegeixes o treus elements, i determinar en quina quantitat es converteix en funció de l’operació aplicada, són destreses imprescindibles per raonar matemàticament.
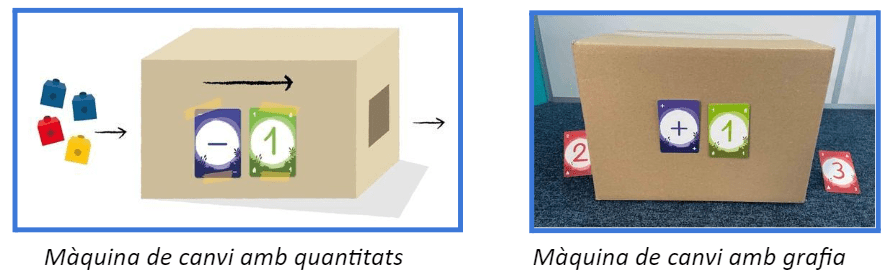
A més, això ens portarà a comprendre que podem cercar diferents maneres de compondre un mateix nombre a partir de la relació entre el tot (per exemple, 6) i les parts (1 i 5; 2 i 4; 3 i 3…).


En definitiva, com veieu, el concepte de nombre té moltes capes que el fan més complex del que sembla a primer cop d’ull. Com a docents, cal ser coneixedors d’aquesta complexitat per dissenyar activitats que permetin treballar-ho des de perspectives diverses.
Com s'aprèn a escriure els números?
Tornem al títol de l’article i centrem-nos ara en el grafisme. D’entrada, ja hem vist que saber com s’escriuen els números és només una petita part del conjunt d’aprenentatges implicats en el concepte global de nombre. I podem preguntar-nos: és important que els infants de 3 a 6 anys llegeixin i escriguin números? La resposta curta és que sí. Però cal afegir algun matís.
Considerem convenient la presència dels números a l’aula. És bo fer-ne esment amb tot allò que hi tingui relació: una dansa que es balla amb 4 persones fent salts de 2 en 2; un conte amb 5 personatges, quants infants són dins la tenda i quants són fora; parelles de quantitats que sumen 6; un joc de punteria amb 7 objectes per descriure quants cauen dins la caixa i quants fora; etc. Aquests, i tants altres, són contextos adequats per llegir i usar els nombres de manera natural, per explicar què ha passat. Vegem-ne alguns exemples fets a les pàgines en blanc.


Ara bé, una cosa és tractar els números que apareixen espontàniament a l’aula amb naturalitat i una altra és formalitzar-ne l’escriptura. Per arribar a escriure correctament els números (i les paraules), cal tenir desenvolupada la motricitat fina, és a dir, la coordinació de moviments que es realitzen entre el cervell, el sistema nerviós i els grups musculars. Escriure els números requereix un alt control i precisió de tots els petits moviments de la mà, els dits, els canells, l’avantbraç i el braç sencer. El desenvolupament de la motricitat fina és un procés lent que depèn d’una maduresa que s’adquireix amb el temps. I aquest temps pot ser diferent per a cada infant, ja que tots tenim un procés maduratiu propi. És ben normal, doncs, que alguns infants necessitin més temps que d’altres. Cada persona és un món, n’hi ha que van més lents que d’altres i no cal preocupar-se, és normal.
A l’escola cal proposar activitats que potenciïn la coordinació entre els ulls i les mans, per desenvolupar el control viso-motriu, afavorir moviments bimanuals, treballar la precisió, regular la força, la tonicitat, la pressió, etc. També és necessari acompanyar els infants a descobrir la seva lateralitat i la direccionalitat i sentit de l’escriptura, per aconseguir el domini progressiu de la psicomotricitat fina amb diferents objectes i eines. Aquest desenvolupament grafomotor es pot treballar a través de propostes d’exploració manipulatives (en la nostra proposta, això passa principalment als Espais).


Ara bé, tinguem en compte que el desenvolupament de la grafomotricitat no és un contingut matemàtic. Les matemàtiques poden crear contextos favorables on practicar aquestes habilitats, però practicar la cal·ligrafia dels números a través de moltes repeticions (com s’ha fet tradicionalment a l’educació infantil) no és fer matemàtiques. De fet, tot i les incomptables repeticions, molts infants arriben als 6 anys i encara escriuen alguns nombres invertits. Per què? Perquè l’escriptura correcta d’aquests numerals no depèn de la quantitat de repeticions, sinó del grau de maduresa de totes les capacitats i habilitats esmentades.
Responem alguns interrogants que ens heu plantejat
- Hem d’ensenyar a escriure els números a infantil?
Sí, però sense una pressió excessiva pel que fa a la representació correcta, que és qüestió de temps. Sempre serà més interessant l’intent d’escriptura d’algun símbol per provar de comunicar una idea matemàtica que no pas un número ben escrit sense cap significat.
- I la part concreta del traç, com la treballem?
Com ho heu fet sempre: convé oferir als infants models de cada nombre; resseguir-los amb paper de vidre (com feia Maria Montessori ja fa cent anys), reproduir-los en safates amb sorra, caminar damunt del grafisme fet a terra, resseguir-lo amb objectes, etc.

- Quins models oferim?
Tenint en compte que les grafies són convencions socials i culturals, serà bo que els infants vegin i reconeguin les grafies més habituals en el seu context (per exemple, tant el 4, com el quatre) i entenguin que es refereixen a la mateixa quantitat. Per tant, entenem que és adequat mostrar, des de l’inici, diferents tipologies de grafies. Pel que fa al model d’escriptura, cada comunitat (país, regió, escola) té els seus referents i, mentre hi hagi coherència, no hi ha evidències que una tipologia sigui millor que una altra.
- És bo corregir les xifres invertides?
Només quan l’infant estigui preparat. Si se n’adona, o ens pregunta com es fa aquest número, és bo tenir sempre a mà un model per poder-lo imitar. Ara bé, si tots els intents d’escriptura de nombres inicials els sancionéssim, els infants deixarien d’assajar l’ús espontani i contextualitzat d’aquests símbols abstractes. També es pot parar especial atenció a la correcció de l’escriptura d’aquests símbols quan, per exemple, aquests apareixen en una carta dirigida a les famílies, en una etiqueta de preu que tots haurem de llegir, en un cartell o informació pública, etc.
Vegem un darrer exemple. A en Pere no li surt l’escriptura del 5, i per això va a cercar-lo entre els models per resseguir.

Se l’emporta a la taula, ratlla el que no ha sortit bé i copia la grafia correcta a sota. Aquesta és l’autonomia que s’hauria de perseguir i, mentrestant, cada docent sap a quin infant i en quin moment té sentit i és adequat dir: «Ep! Veig un número del revés, el vols trobar i arreglar?».
Per tancar
La construcció del concepte de nombre inclou una gran varietat de coneixements de naturaleses diferents. La lectura i escriptura de les grafies és una petita part d’aquest gran constructe, i no n’és la principal. És important que els números (grafies) estiguin presents a les nostres aules i que els vinculem amb situacions amb significat, contextualitzades. Té sentit convidar els infants a representar aquestes situacions viscudes usant aquells llenguatges que estan aprenent, sigui pictogràfic, verbal o simbòlic. Però hem de ser conscients del que requereix representar «correctament» els símbols, i no exigir o focalitzar mai el treball matemàtic d’aquestes edats en la representació correcta dels números escrits. Per tot plegat, proposem que es faci la iniciació al desenvolupament del traç i de la grafia des del moviment lliure i, sempre que es pugui, en situacions significatives i funcionals.
Una activitat per treballar la grafia
Prova Innovamat durant 30 dies.
Si no tens un compte d'Innovamat i vols provar totes les activitats que hi ha a continuació, prova gratuïtament la proposta durant 30 dies.
Canals, M.A. (1989). Per una didàctica de la matemàtica a l’escola. Eumo.
Dickson, L., Brown, M., y Gibson, O. (1991). El aprendizaje de las matemáticas. Labor-MEC.
Kamii, C. (1983). El número en la educación preescolar. Visor.
Piaget, J. (1952). The Child’s Conception of Number. Routledge.
Schaeffer, B., Eggleston, V. H., & Scott, J. L. (1974). Number development in young children. Cognitive Psychology, 6(3), 357–379.






