È così che di solito inizio le mie sessioni di sviluppo professionale sulla matematica per la scuola primaria e il mio corso di formazione per insegnanti all’università. Chiedo semplicemente: “Cos’è un problema?“.
Voi cosa ne pensate?
Faccio questa domanda per rompere il ghiaccio e per esplorare il modo in cui le persone in classe interpretano una parola dai molteplici significati, che ha valicato da tempo i confini della matematica e ha trovato posto nel lessico di tutti giorni. Capire il significato di questa parola è fondamentale se vogliamo addentrarci nelle indicazioni nazionali per il curricolo, nelle metodologie matematiche, nelle linee guida per l’insegnamento e nei programmi che mettono in primo piano il problem solving, plasmando il modo in cui ci avviciniamo all’insegnamento della matematica. Ecco alcune delle risposte più comuni che ricevo:
“Una consegna che implica un’operazione di calcolo”.
“Un’attività con un contesto”.
“Una qualsiasi cosa da risolvere”.
“Ciò che richiede tempo per essere risolto”.
Di solito si tratta di una combinazione di queste risposte. Pertanto, oriento la conversazione stilando un elenco con le caratteristiche del problema:
- Consegna scritta (o enunciato)
- Calcolo
- Contesto
- Con una soluzione
- Richiede tempo
Poi chiedo di farmi un esempio. Durante la mia ultima sessione di formazione, mi è stato detto:
Oggi a pranzo saremo in 7. Se sappiamo che ogni persona mangerà 2 panini, quanti panini dovremo preparare in totale?
Diamo un’occhiata al nostro elenco: c’è una consegna scritta che implica un calcolo, un contesto con riferimenti alla vita reale e anche la richiesta di ricerca di una soluzione. Per trovare una risposta ci vorrà poco tempo, ma solo perché gli ospiti sono pochi e non hanno molta fame, giusto?
Bene, se diamo un’occhiata al nostro elenco, a quanto pare, siamo davvero di fronte a un problema. A questo punto, chiedo ai presenti di risolverlo.
“Allora, quanti panini prepareremo?”.
“14”.
“Perché?”.
Mi guardano come se avessi chiesto se il cielo è blu.
“Perché ovviamente dobbiamo fare sette per due”.
“Ovviamente, sono d’accordo. Allora, fare questo calcolo è un problema per voi?”.
Mentre pensano alla risposta, scrivo rapidamente alla lavagna:

E dico: “Se vi chiedessi di risolvere questa equazione, sarebbe un problema per voi?”
Molti iniziano a ridere nervosamente prima di rispondere. Ma non ha un contesto, non c’è una consegna con delle parole vere e proprie…
Capite dove sto andando a parare, vero? Anche le persone in aula hanno iniziato a capire. Si sono resi conto che la loro risposta, e l’elenco delle caratteristiche, è falsata dalla tradizione scolastica di come trattiamo i cosiddetti problemi a parole.
Il pericolo è che, ogni volta che leggiamo le parole problema o problem solving nelle indicazioni nazionali o in altre risorse, potrebbe sfuggirci il loro vero significato. Come possiamo sviluppare competenze di problem solving se ne fraintendiamo la definizione?

Cosa dice la ricerca
Vediamo brevemente il parere di alcuni autori di riferimento. In un recente articolo di grande interesse, Foster (2023, p. 2) spiega che consideriamo attività matematica qualsiasi operazione matematica che chiediamo ai nostri alunni di eseguire, facendo una distinzione tra attività di routine e attività non di routine. Le attività di routine, chiamate esercizi, servono agli alunni a imitare un metodo che è stato loro insegnato. Un’attività o un problema non di routine è “un’attività per la quale la metodologia di risoluzione non è nota a priori” (NCTM, 2000, p. 52). Liljedahl (2020, p. 26) lo scrive in termini ancora più semplici: “Il problem solving è ciò che facciamo quando non sappiamo cosa fare“.
Pertanto, se un’attività è o meno un problema dipende principalmente dal fatto che la persona che la affronta abbia già una strategia di risoluzione (oppure no). Attenzione: la distinzione tra esercizio e problema è slegata dall’impegno richiesto per risolverli. Foster spiega anche che (2023, p. 4), “Un’attività può essere di routine ma difficile. Ad esempio, moltiplicare due numeri di 5 cifre può essere un compito complesso, ma completamente di routine per chi conosce bene l’algoritmo di moltiplicazione”.
Torniamo alla parola “problema” relativamente all’esempio dei panini. È davvero un problema? Per un bambino di primo anno di scola primaria che non conosce bene le addizioni, potrebbe essere una situazione non di routine, quindi un problema. Quando avrà imparato a leggere e riuscirà a comprendere la consegna, sarà solo un altro esercizio per fare pratica con le moltiplicazioni. La maggior parte delle attività che oggi per noi sono problemi, saranno esercizi man mano che sviluppiamo competenze di problem solving.
Questo accade sempre? Sì e no. Ovviamente, bisogna sempre tenere conto delle competenze della persona, ma ciò non significa necessariamente che non si possano trovare attività utili a sviluppare competenze di problem solving in base alle diverse fasi dell’apprendimento o età. Prendiamo l’esempio classico delle viste:
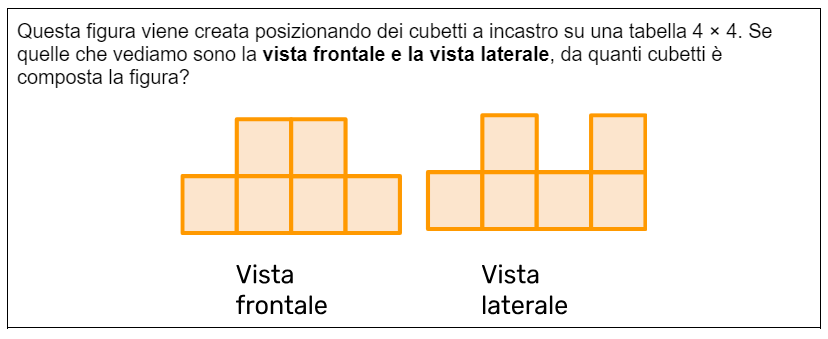
Gli alunni di scuola dell’infanzia possono riflettere sull’attività provando e creando soluzioni con l’uso dei materiali manipolativi, e ci riterremo soddisfatti se trovano anche una sola soluzione possibile. Gli alunni più grandi, e anche le persone adulte, possono avere difficoltà nel trovare tutte le soluzioni possibili. Qual è la quantità massima di cubetti? E la quantità minima? Possiamo realizzare questa figura con un numero qualsiasi di cubetti compresi tra queste quantità? E così via. Naturalmente, anche il modo in cui poniamo le domande in classe è fondamentale, ma esploreremo questo aspetto nei prossimi articoli.
In ogni caso, la mia esperienza mi ha insegnato che queste attività sono le migliori da condividere con gli insegnanti nel corso di una sessione di sviluppo professionale. Ci fanno riflettere, ci mettono alla prova e ci fanno capire cosa significa risolvere i problemi. In altre parole, ci fanno pensare in modo matematico, il che è un bene.
Perché i problemi sono così importanti?
Tempo fa ho scritto che i problemi stanno all’attività matematica come le montagne stanno all’alpinismo. Rappresentano la vetta, ma anche il viaggio, il percorso verso la cima, la strada da percorrere per ottenere la ricompensa finale: panorami e una vista mozzafiato. Sono una sfida che aspetta solo di essere superata, sono indispensabili. Risolvere un problema per il quale si è lottato dà una grande soddisfazione e l’interesse nel volerlo risolvere deriva direttamente da questa sensazione.
Dovremmo eliminare gli esercizi nelle lezioni di matematica? Dipende dagli obiettivi che ci prefissiamo. Gli esercizi sono interessanti se vogliamo che i nostri alunni facciano pratica con algoritmi e procedimenti. I “problemi” a parole sono fondamentali per esercitare anche la comprensione del testo. Inoltre, molti test nazionali ufficiali si concentrano ancora su queste attività, quindi per il momento è bene che i nostri alunni le conoscano. Come diciamo sempre noi di Innovamat, anzitutto evitate di dedicare tutto il vostro tempo allo stesso tipo di attività di routine. Siate aperti di mente, provate cose nuove. E soprattutto, ricordate che la matematica è molto più che semplici numeri e operazioni.


In fin dei conti, la maggior parte del tempo in classe dovrebbe essere dedicato al “problem solving“, quello che Liljedahl (2020) chiama “thinking classrooms” (classi pensanti), dove si discute, si argomenta, si cercano strategie, collegamenti e ragionamenti. Come dice l’autore, “il problem solving è un processo disordinato, non lineare e peculiare. Gli alunni trovano un ostacolo, quindi iniziano a pensare. E così superano l’ostacolo. E quando lo fanno, imparano a conoscere la matematica, a conoscere se stessi e a pensare”. (Liljedahl, 2020, p. 20)
Ora magari vi starete preoccupando perché pensate che la maggior parte delle vostre attività sia composta da esercizi (compresi i problemi a parole). Cosa potete fare al riguardo? Nel lungo periodo, lavorate per creare un ambiente di risoluzione di problemi. A breve termine, invece, vi invito a esaminare quattro strategie per arricchire e riutilizzare alcuni di questi esercizi tradizionali, attraverso degli esempi.
Riferimenti bibliografici
Foster, C. (2023). Problem solving in the mathematics curriculum: From domain‐general strategies to domain‐specific tactics. The Curriculum Journal, 213. https://doi.org/10.1002/curj.213
Liljedahl, P. (2020). Building thinking classrooms in mathematics, grades K-12: 14 Teaching Practices for Enhancing Learning. Corwin Mathematics.
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. NCTM.
Ulteriori riferimenti bibliografici
Hiebert, J., & Wearne, D. (2003). Developing understanding through problem solving. In Schoen, H. L. i Charles, R. I. (Eds.), Teaching mathematics through problem solving (pp. 6–12). Reston, VA: NCTM.
Pólya, G. (1945). How to solve it. Princeton University Press.
Schoenfeld, A. (1992). Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. In Grouws D. A. (Ed.), Handbook for Research on Mathematics Teaching and Learning. Macmillan Publishing Company.
Schoenfeld, A. H. (2007). Problem solving in the United States, 1970–2008: Research and theory, practice and politics. ZDM, 39(5), 537-551. https://doi.org/10.1007/s11858-007-0038-z
Schoenfeld, A. H. (2014). Mathematical Problem Solving. Elsevier Gezondheidszorg.






