È davvero necessario imparare le tabelline a memoria? È giusto incoraggiare lo sforzo matematico? E la pratica, è importante?
Queste sono solo alcune delle domande che spesso ci fate arrivate; e noi le abbiamo trasformate in… un gioco!
1/5 È cambiato il modo di risolvere le operazioni di base?
Risolviamo le operazioni come chiunque altro; cambia solo il modo di apprenderle.
Perché gli alunni acquisiscano fluidità nella risoluzione delle operazioni e trovino il risultato corretto in modo efficiente, è necessario costruirle promuovendo una comprensione profonda: cosa stiamo facendo e perché funziona?
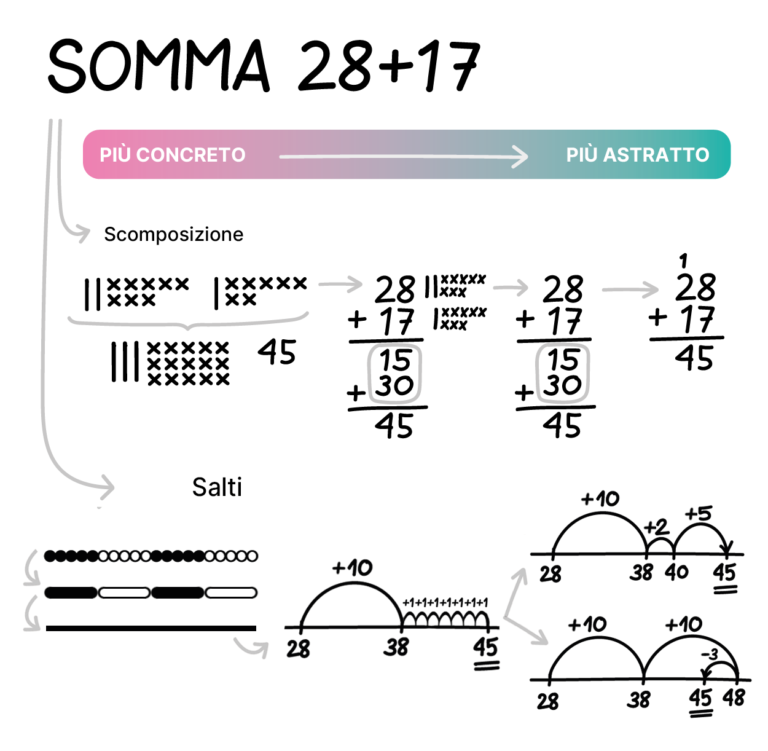
Per costruire in modo significativo le operazioni di base (addizione, sottrazione, moltiplicazione e divisione), introduciamo diverse strategie. Padroneggiare diverse strategie di calcolo, oltre ad aumentare la comprensione, favorisce la flessibilità.
Ognuna di queste strategie prevede un processo di apprendimento che ne massimizza la comprensione. Partiamo sempre dall’esplorazione degli aspetti più concreti attraverso l’uso di materiali manipolativi e arriviamo all’astrazione con rappresentazioni più efficienti e sintetiche.
- Van Den Heuvel-Panhuizen, M. (2008). Children Learn Mathematics: A Learning-Teaching Trajectory with Intermediate Attainment Targets for Calculation with Whole Numbers in Primary School. Dutch Design in Mathematics Education, Vol. 1. Utrecht: Freudenthal Institute, Sense Publishers.
-
Kilpatrick, J., Swafford, J., Findell, B., & National Research Council (U.S.), Mathematics Learning Study Committee. (2001). Adding it up: Helping children learn mathematics. National Academy Press.
2/5 Esercitarsi è importante?

Esercitarsi è essenziale per consolidare le conoscenze e acquisire fluidità matematica.
Pertanto, è importante dedicare momenti alla pratica riproduttiva focalizzata sul raggiungimento della padronanza di una procedura specifica attraverso la sua ripetizione. Anche la pratica produttiva, dove esercitarsi diventa pretesto per rafforzare il lavoro sui processi matematici come la risoluzione di problemi, è fondamentale.
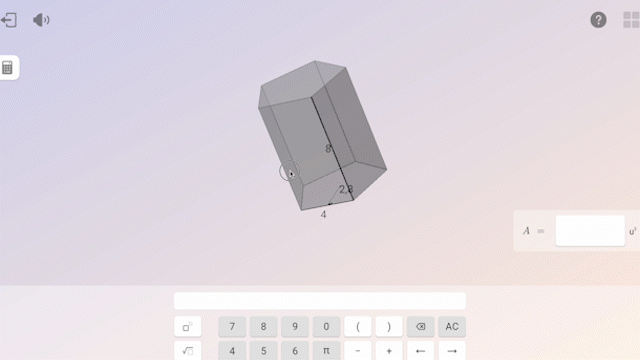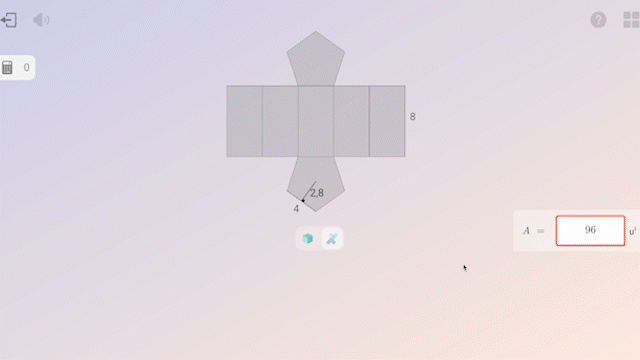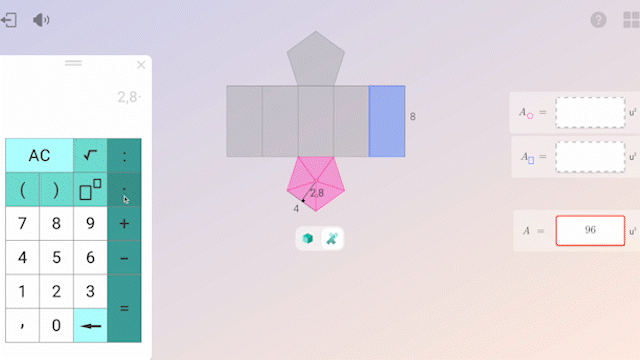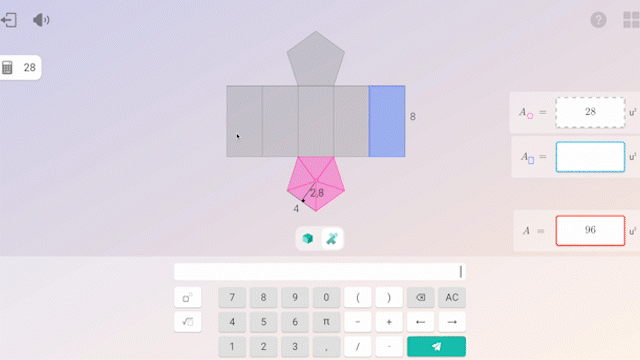
In questo contesto, l’uso della tecnologia apporta un grande valore aggiunto: permette di individualizzare l’apprendimento, fornendo feedback immediati e report dettagliati sui progressi di ogni alunno. Ciò consente agli insegnanti di accompagnare gli alunni più da vicino.

- Spangler, D. A., & Wanko, J. J. (2017). Enhancing Classroom Practice with Research Behind Principles to Actions. NCTM.
-
Pettersson, F. (2017). On the issues of digital competence in educational contexts – a review of literature. Education and Information Technologies, 23(3), 1005–1021. https://doi.org/10.1007/s10639-017-9649-3
3/5 Le tabelline devono essere imparate a memoria?

L’automatizzazione delle tabelline è imprescindibile affinché l’apprendimento dei concetti correlati, come divisioni e potenze, su cui si lavorerà più avanti, sia significativo.
Dopo aver costruito le tabelline, bisogna automatizzarle (attraverso la pratica) e sviluppare strategie che permettano di dedurre rapidamente i risultati non ancora memorizzati a partire da quelli già conosciuti.
Gli alunni che non conoscono le tabelline sperimentano un sovraccarico cognitivo nella risoluzione di problemi avanzati: dedicano tempo ed energie ai calcoli di base, sottraendo risorse all’analisi di aspetti più complessi.
-
Bay-Williams, J. M., & SanGiovanni, J. J. (2022). Accessing Fluency through Routine and Opportunity. NCTM Annual Meeting 2022. Los Angeles.
-
Vilalta, A., Calvo, C., & Correig, E. (2023). Automatizar las tablas de multiplicar: un propósito que va más allá de 3.º EP. UNO: Revista de Didáctica de las Matemáticas, 99, 61-67.
-
Sweller, J. (1988). Cognitive load during problem solving: Effects on learning. Cognitive Science, 12(2), 257-285.
4/5 Dovremmo proporre un apprendimento della matematica privo di sforzo?

Lo sforzo (dall’inglese, struggle) nell’apprendimento della matematica non va evitato, ma anzi usato per imparare. Lo sforzo produttivo (productive struggle) consiste nel rafforzamento della perseveranza e della flessibilità di pensiero e non si limita alla semplice ricerca della soluzione corretta.
Noi insegnanti moduliamo questo sforzo ponendo agli alunni sfide adeguate, senza dare risposte dirette e promuovendo la motivazione e l’autonomia.
Avere una mentalità di crescita è essenziale per trasformare gli errori in opportunità di miglioramento, sviluppare la resilienza e mantenere alta la motivazione durante il processo di apprendimento.
- Boaler, J. (2016). Mathematical Mindsets: Unleashing Students’ Potential through Creative Math, Inspiring Messages, and Innovative Teaching. Jossey-Bass.
-
Dweck, C. S. (2006). Mindset: The New Psychology of Success. Random House.
5/5 Il ruolo di noi insegnanti è rilevante nel processo di apprendimento?

Nessuna risorsa o materiale, per quanto valido o di qualità, può risultare efficace senza l’impegno degli insegnanti.
Non ci sono formule magiche: l’impegno, la formazione continua e la fiducia nel potenziale degli alunni sono i veri elementi chiave del loro apprendimento.
Le guide didattiche e le opportunità formative sono strumenti preziosi per crescere come professionisti e offrire la migliore esperienza educativa possibile.
-
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1), 1-22.
-
Darling-Hammond, L. (2000). Teacher quality and student achievement: A review of state policy evidence. Education Policy Analysis Archives, 8(1), 1-44.
Se questo articolo ti è piaciuto, consulta il nostro libro bianco, dove esploriamo queste e altre tematiche in modo più approfondito.
Siamo qui per aiutarti e lavorare insieme per migliorare l’apprendimento della matematica.
A presto!





