Descarrega el nou Ebook
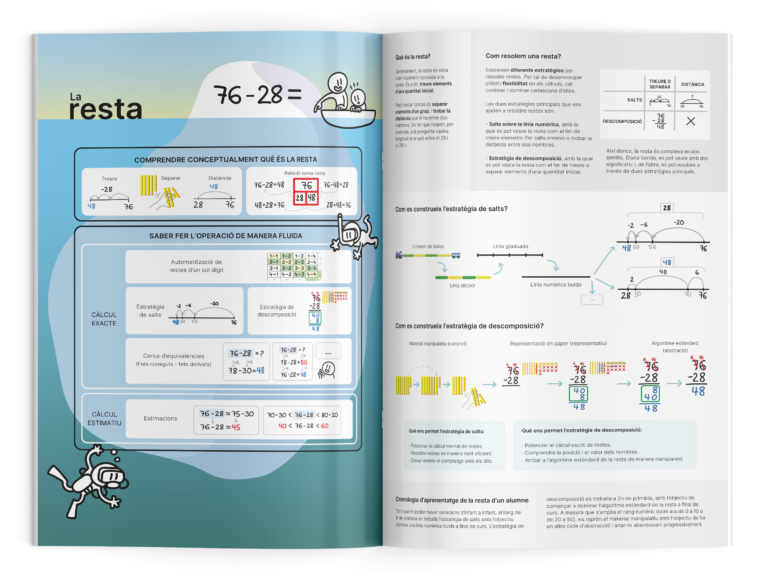
Explora aquest recurs que sintetitza de manera visual algunes de les estratègies més utilitzades de les operacions bàsiques.

Articles relacionats:
- La suma (pròximament)
- La resta (pròximament)
- La multiplicació (pròximament)
- La divisió (pròximament)
Sabem que les matemàtiques no són només operacions, però ¿què és més important per a l’aprenentatge d’aquesta part fonamental de les matemàtiques: entendre el que fem, arribar al resultat correcte o resoldre les operacions en un temps raonable?
Com a docents, les expectatives en l’aprenentatge dels nostres alumnes han de ser altes. Així que ho hem de voler tot!
- Els alumnes han d’entendre què fan i per què.
- Han d’arribar al resultat correcte aplicant els procediments correctament.
- I també han de resoldre les operacions de manera eficient i en un temps raonable.
Com veieu, la resposta no és excloent: tots tres objectius són indispensables. Ara bé, som conscients que és un objectiu ambiciós. Sobretot quan gestionem l’aula d’un grup d’alumnes que tot just emprenen el camí en les matemàtiques.
Així doncs, en aquest article explorem com abordar l’aprenentatge de les matemàtiques per assolir fluïdesa.
Entendre abans d’aplicar o aplicar abans d’entendre?
Peter Liljedahl, en el llibre Diseñando aulas para pensar en matemáticas, proposa 14 pràctiques per fomentar la participació dels alumnes i aconseguir que pensin. Aquestes pràctiques estan orientades a crear aules on els estudiants siguin els veritables protagonistes, convidant-los a anar més enllà de la simple repetició mecànica.
Per què hauríem de fomentar aules on els alumnes només executin mecànicament allò que podria fer millor i més ràpidament una màquina? En canvi, quan un alumne entén conceptes com què vol dir restar o per què fem servir determinades estratègies, com els salts sobre la línia numèrica, obté una base més sòlida per als nous aprenentatges.
Ara bé, posar el focus en la comprensió no significa que no hagin de resoldre les operacions correctament. Sí que han d’arribar al resultat correcte. Per això a l’aula també es dedica temps a la pràctica per consolidar els aprenentatges i guanyar fluïdesa.

Dins d’aquest context, el paper del mestre com a guia és indispensable. El mestre ha d’ajudar a descobrir les estratègies de manera clara i transparent. I, després, assegurar-se que els alumnes continuen consolidant els continguts a través de la pràctica, animant-los a sortir de la seva zona de confort i incrementant gradualment la dificultat dels reptes i procediments.
Per exemple, quan un alumne ha resolt correctament algunes restes (depenent de cada infant) utilitzant material manipulatiu, és moment de convidar-lo a treballar sense aquest material, però utilitzant representacions visuals. Després, quan hagi resolt correctament algunes operacions més amb aquest nou enfocament, hem de retirar, de nou, aquestes bastides, i acompanyar-lo a fer un canvi de representació cada cop més abstracte. I així successivament.
Aquests suports, o bastides, són essencials en les primeres fases de l’aprenentatge. Però han de desaparèixer gradualment perquè l’alumne assoleixi un pensament més abstracte i vagi guanyant fluïdesa. L’objectiu és completar el recorregut fins que pugui resoldre les operacions sense cap mena de suport. Però, això sí, tenint estratègies a les quals recórrer en cas que ho necessiti.
Construcció d’estratègies basada en el model CRA
Cadascuna de les estratègies segueix una seqüència d’aprenentatge concreta basada en la comprensió: què estem fent.
Per això, seguim el model CRA (concret, representatiu, abstracte), una metodologia d’aprenentatge matemàtic basada en tres etapes progressives que ajuden els estudiants a comprendre i dominar els conceptes matemàtics.
Primer, partim de la manipulació amb diferents materials (concret); a continuació, representem en paper el que fèiem manipulativament (representatiu), i, finalment, passem a les representacions abstractes, com els algoritmes (abstracte).
Què entenem per fluïdesa?
La recerca defineix la fluïdesa com l’habilitat de treballar amb nombres, operacions i procediments amb soltesa.
La fluïdesa té tres nivells de profunditat:
Fluïdesa factual (fact fluency): habilitat per evocar fets coneguts o derivats amb soltesa gràcies a l’automatització. Dins d’aquest marc entra l’automatització de sumes d’un dígit, a 1r i 2n de primària (7 + 3 = 10; 6 + 4 = 10; 8 + 7 = 15), i l’automatització de les multiplicacions d’un dígit (taules de multiplicar), a 3r i 4t de primària.
Fluïdesa computacional (computational fluency): habilitat per fer operacions (computar), amb soltesa, més enllà de les operacions simples. Dins d’aquest marc entren habilitats tan clau que van des d’executar correctament l’estratègia de salts fins al model de repartiments de la divisió.
Fluïdesa procedimental (procedural fluency): habilitat per seguir amb soltesa procediments que van més enllà d’una operació bàsica i que depenen de cada etapa. Aquí ens referim a trobar el mcm, resoldre operacions combinades, resoldre equacions, etc.
A més, dins de la definició de fluïdesa, existeixen tres components clau i sis accions relacionades:
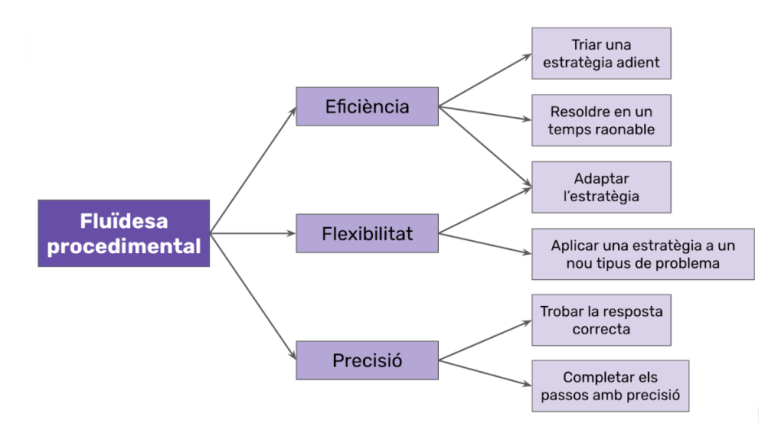
Com veieu, tenir fluïdesa no només és resoldre operacions ràpidament. També implica ser eficient i flexible a l’hora d’escollir una estratègia, adaptar-la segons el context i arribar al resultat correcte, completant els passos amb precisió.
Quins fets s’han de saber respondre amb rapidesa?
Sovint, quan parlem d’un aprenentatge basat en la comprensió profunda dels coneixements, sembla que demonitzem completament la velocitat en la resposta, però hi ha diferents continguts que haurien de formar part del coneixement automàtic dels alumnes. Són:
- L’automatització de sumes d’un dígit (rang 0-10)
- L’automatització de les multiplicacions d’un dígit (taules de multiplicar)
De fet, són alguns dels continguts que entren dins del marc de la fluïdesa factual. El fet de no saber respondre ràpidament i, encara més, no tenir estratègies eficients per deduir els resultats, comporta que els infants hagin de dedicar esforços a càlculs bàsics, reduint la capacitat de concentrar-se en aspectes més avançats o complexos.
Per això és important saber respondre de pressa, ja sigui perquè ens ho sabem de memòria o perquè ho hem deduït molt ràpidament a partir d’uns quants resultats bàsics sense gaire esforç. Per exemple, un alumne pot deduir molt ràpidament 60 + 70 = 130 de 6 + 7 = 13.
Com podem aconseguir eficiència i flexibilitat a partir de la construcció de diverses estratègies
Com hem vist, un dels pilars per desenvolupar fluïdesa és conèixer diferents maneres d’enfrontar les operacions. És a dir, dominar diverses estratègies que ens permetin resoldre qualsevol operació depenent del context i dels nombres implicats. En definitiva, tenir flexibilitat.
Fixem-nos en les sumes i restes, per exemple. De vegades, convé fer servir l’algoritme escrit. D’altres, preferim fer un càlcul mental tot imaginant salts sobre la línia numèrica. També hi ha moments en què podem deduir el resultat a partir de fets que ja coneixem. Fins i tot hi ha ocasions en què volem emprar la calculadora.
Conèixer aquesta varietat, i saber triar, és el que ens fa ser flexibles i eficients a l’hora de calcular. Tanmateix, la pràctica és la que ens ajudarà a guanyar agilitat en l’execució.
L’aprenentatge significatiu de les operacions bàsiques
L’aprenentatge de les matemàtiques (sobretot la part de numeració) té una estructura jeràrquica: cal trepitjar un contingut per poder avançar cap al següent. Les operacions bàsiques (suma, resta, multiplicació i divisió) són fonamentals en aquest procés, ja que aplanen el terreny per sembrar-hi altres conceptes més avançats de numeració i o àlgebra.
Més enllà dels algoritmes, dominar cada operació bàsica implica entendre’n el significat, saber com es resol i quines estratègies podem utilitzar per aconseguir-ho.
Cada operació és com un iceberg: el que veiem a la superfície és només una petita part de tota la complexitat. Tot el que es manté sota l’aigua és el que dona suport i sentit en el domini de cada operació.
Així doncs, hem ideat aquest recurs. Un llibret que resumeix de manera sintètica i visual tot el que amaga l’aprenentatge de cada operació bàsica:
- Què vol dir sumar, restar, multiplicar i dividir.
- Quines estratègies es proposen per resoldre cada operació.
- Quina seqüència d’aprenentatge, basada en el model CRA, segueix cada estratègia.
Tenir aquest coneixement ens permetrà ser més flexibles i eficients. Tot i això, practicar serà essencial per guanyar rapidesa en els càlculs, un aspecte que treballarem més endavant.
De moment, et convidem a submergir-te en aquest recurs i a explorar-ne les profunditats per convertir l’aprenentatge de cada operació en una oportunitat per pensar, entendre i progressar.
Descarrega el nou Ebook
Explora aquest recurs que sintetitza de manera visual algunes de les estratègies més utilitzades de les operacions bàsiques.

Referències bibliogràfiques
- Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22-31.
- Bay-Williams, J. M., y SanGiovanni, J. J. (2021). Figuring out fluency: Mathematics teaching and learning, grades K-8: Moving beyond basic facts and memorization (1st ed.). Corwin.
- Hmelo‐Silver, C. E., Duncan, R. G., y Chinn, C. A. (2007). Scaffolding achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 99–107. https://doi.org/10.1080/0046150701263368
- Van den Heuvel-Panhuizen, M. (2008). Children learn mathematics: Learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Dutch design in mathematics education, V: 1. Utrecht: Freudenthal Institute, Sense Publishers.