Horrela hasi ohi ditut Lehen Hezkuntzako irakasleentzako matematikako prestakuntza-saioak eta irakasleen prestakuntzarako unibertsitate-ikastaroa. Honela galdetu ohi dut: «Zer da problema bat?».
Eta zer da zuentzat?
Galdera horrek, izotza hausten ez ezik, entzuleek esanahi anitz dituen hitz bat nola ulertzen duten aztertzen laguntzen dit; hitz horrek, izan ere, aspaldi utzi zion esanahi matematikoa soilik izateari, eta, gaur egun, gure eguneroko hiztegiaren parte da. Horrez gain, gako-hitz ezin garrantzitsuagoa da tokiko estandarrei, matematika-praktikei, irakaskuntza-jarraibideei eta problemak ebaztea ardatz duten programei begira, matematika irakasteko moduari buruzko informazioa ematen digulako. Hona hemen jaso ohi ditudan erantzunetako batzuk:
«Idatzizko enuntziatu bat da, eta egin beharreko eragiketa aurkezten du».
«Testuinguruan kokatutako zeregin bat da».
«Ebatzi beharreko edozer gauza da».
«Ebazteko denbora eskatzen duen gauza oro da».
Orokorrean, problema bat erantzun horien guztien konbinazioa da. Jarraian, eztabaida arretaz gidatu ohi dut problemen ezaugarrien zerrenda egiteko:
- Enuntziatua
- Kalkulua
- Testuingurua
- Erantzun bat du
- Denbora hartzen du
Ondoren, adibide bat eskatu ohi dut. Eman nuen azken prestakuntza-saioan, honako adibide hau proposatu zidaten:
Gaur 7 lagun izango gara bazkaltzeko. Lagun bakoitzak 2 ogitarteko jango dituela badakigu, zenbat ogitarteko prestatu behar ditugu?
Eta, idatzi ahala, honela esan nuen: «Orain arbelera gerturatu eta honako hau ebazteko eskatuko banizueke, problema bat izango al litzateke zuentzat?».
Batzuek barre egin zuten, urduri, eta onartu zuten baietz, hala izango litzatekeela. Baina ez zuen testuingururik, ezta enuntziaturik ere…
Badakizue zer esan nahi dudan, ezta? Bada, entzuleek ere bazekiten. Konturatu ziren beren erantzunak eta ezaugarri-zerrenda baldintzatuta zeudela: irakaskuntzan, tradizioz, PAES (Problemas de Aritmética Escolar) gisa ezagutzen direnek baldintzatuta.
Eta horrek badu arrisku handi bat: estandar ofizialetan edo beste edozein baliabidetan problema edo problemak ebaztea hitzak irakurtzen ditugun bakoitzean, haien egiazko esanahia galtzeko arriskua dugu. Baina, orduan, nola susta ditzakegu problemak ebazteko trebetasunak, hitzaren esanahia behar bezala interpretatzen ez badugu? 
Zer diote ikerketek?
Ikus dezagun, labur-labur bada ere, zer dioten erreferentziazko egile batzuek. Duela gutxi argitaratutako artikulu bikain batean, Foster-ek (2023, 2. orr.) azaltzen du zeregin matematikoak, guretzat, ikasleei eskatzen diegun gauza matematiko oro direla, eta, hala, zeregin horiek honela bereizten ditugu: ohiko zereginak eta ezohiko zereginak. Ohiko zereginak (ariketak ere deituak) gonbidapen modukoak dira, eta, horietan, ikasleei aurrez irakatsi diegun metodo bat imitatzeko eskatzen zaie. Horrenbestez, ezohiko zeregin edo problema batek zera izan behar du: «ebazpen-metodoa ezezaguna duen zeregina» (NCTM, 2000, 52. orr.). Liljedahl-ek (2020, 26. orr.) are definizio sinpleagoa proposatzen du: «problemak ebaztea deritzo zer egin ez dakigunean egiten dugun horri».
Beraz, zeregin bat problema izan dadin, hura ebazteko estrategiarik ba ote dugun edo ez begiratu behar dugu batez ere. Baina, kontuz! Ariketa eta problemaren arteko alde horrek ez du zerikusirik zeregina ebazteko egin behar den ahaleginarekin. Foster-ek (2023, 4. orr.) dioen moduan: «Zeregin bat ohikoa izan daiteke, baina ez du zertan erreza izan. Esate baterako, 5 digituko bi zenbaki biderkatzea zaila izango litzateke, baina guztiz ohikoa biderketa luzeen algoritmoa ondo ezagutzen duen norbaitentzat».
Itzul gaitezen ogitartekoen «problemara». Problema bat al da benetan? 1. mailako ikaslea bazara eta oraindik ez badituzu batuketak behar bezala egiten, baliteke zuretzat oraindik ohikoa ez izatea. Kasu horretan, beraz, zuretzat problema izango litzateke. Aldiz, enuntziatua irakurtzeko eta ulertzeko gai zarenean, biderketa lantzeko ariketa bat baino ez da izango. Orain guretzat problema diren zeregin gehienak, denborarekin, problemak ebazteko trebetasunak garatu ahala, ariketa izatera igaroko dira.
Eta hori beti al da horrela? Bada, bai, eta ez. Jakina, problema ebazten duen pertsonaren trebetasunak hartu behar dira kontuan, baina horrek ez du zertan esan nahi hainbat maila edo adinetan problemak ebazteko trebetasunak garatzeko egokiak diren zereginak aurkitu ezin ditugunik. Azter dezagun bisten adibide klasiko hau:
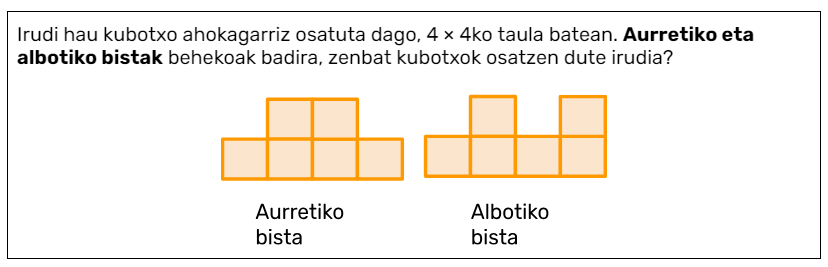
HHko 5. mailako edo LHko 1. mailako ikasleak zeregina nola egin dezaketen pentsatzen has daitezke, probak egin ditzakete eta kontzeptuak eraiki ditzakete materiala manipulatuz. Eta pozik egon gaitezke erantzun posible bat aurkitzen badute. Nagusiagoak diren ikasleek, berriz, eta baita helduek ere, zailtasunak izan ditzakete erantzun guztiak aurkitzeko. Zein da gehieneko kubo kopurua? Eta gutxienekoa? Irudia tarteko edozein kubo kopururekin eraiki al dezakegu? Etab. Ikasgelan galderak egiteko modua ere oso garrantzitsua da, baina hori beste artikulu batean aztertuko dugu.
Nolanahi ere, esperientziak irakatsi dit era horretako zereginak direla prestakuntza-saioetan irakasleekin partekatzeko onenak. Problemak ebaztea zertan datzan pentsatzera eta, azken batean, sentitzera animatzen gaituzte, eta, beraz, matematikoki pentsatzea zer den pentsatu eta sentitzera. Eta hori zoragarria da.
Zergatik dira problemak horren garrantzitsuak?
Denborarekin, ikasgelan ematen dugun denbora gehiena problemak ebazten eman beharko genuke —Liljedahl-ek (2020) pentsamendu-ikasgela deitzen dio horri—; izan ere, une horietan sortzen dira eztabaidak, argudiaketak, estrategiak bilatzea, loturak eta arrazoiketak. Egileak dioen moduan, «problemak ebazteko prozesua nahasia, ez-lineala eta idiosinkrasikoa da. Ikasleak trabatu egingo dira. Pentsatu egingo dute. Eta trabak gaindituko dituzte. Eta hori gertatzen denean, ikasi egingo dute: matematikari buruz, beren buruari buruz eta pentsatzen ikasiko dute» (Liljedahl, 2020, 20. orr.).
Hala, baliteke orain beste kezka bat izatea gogoan: ikasgelan proposatzen ditugun zeregin gehienak ariketak dira (testuinguruan kokatutako egoerak barne). Zer egin dezakegu horren inguruan? Epe luzera, ikasgelan problemak ebazteko giroa sustatzen saiatu. Eta, epe laburrera, ohiko ariketa horietako batzuk aberastu eta birziklatzeko lau estrategia ikustera gonbidatzen zaituztet, adibideen bidez.
Referencias
Foster, C. (2023). Problem solving in the mathematics curriculum: From domain‐general strategies to domain‐specific tactics. The Curriculum Journal, 213. https://doi.org/10.1002/curj.213
Liljedahl, P. (2020). Building thinking classrooms in mathematics, grades K-12: 14 Teaching Practices for Enhancing Learning. Corwin Mathematics.
National Council of Teachers of Mathematics (NCTM). (2000). Principles and standards for school mathematics. NCTM.
Otras referencias
Hiebert, J., & Wearne, D. (2003). Developing understanding through problem solving. In Schoen, H. L. i Charles, R. I. (Eds.), Teaching mathematics through problem solving (pp. 6–12). Reston, VA: NCTM.
Pólya, G. (1945). How to solve it. Princeton University Press.
Schoenfeld, A. (1992). Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics. In Grouws D. A. (Ed.), Handbook for Research on Mathematics Teaching and Learning. Macmillan Publishing Company.
Schoenfeld, A. H. (2007). Problem solving in the United States, 1970–2008: Research and theory, practice and politics. ZDM, 39(5), 537-551. https://doi.org/10.1007/s11858-007-0038-z
Schoenfeld, A. H. (2014). Mathematical Problem Solving. Elsevier Gezondheidszorg.
