Deskargatu liburu elektronikoa
Ezagutu baliabide hau, oinarrizko eragiketetan gehien erabiltzen diren estrategiak modu bisualean laburbiltzen dituena.

Erlazionatutako artikuluak:
- batuketa (laster eskuragarri)
- kenketa (laster eskuragarri)
- biderketa (laster eskuragarri)
- zatiketa (laster eskuragarri)
Badakigu matematika eragiketak egitea baino askoz gehiago dela, baina ezin dugu ahaztu eragiketak oinarri-oinarrizkoak direla matematikan. Beraz, zer da garrantzitsuagoa: egiten duguna ulertzea, emaitza zuzena lortzea edo eragiketak arrazoizko denboran ebaztea?
Irakasle gisa, gure ikasleen ikaskuntzan itxaropen handia izan behar dugu. Beraz, anbiziotsuak izan behar dugu!
- Ikasleek zer egiten duten eta zergatik egiten duten ulertu behar dute.
- Emaitza zuzenera iritsi behar dute, prozedurak behar bezala aplikatuz.
- Gainera, eragiketak modu eraginkorrean ebatzi behar dituzte, eta arrazoizko denboran.
Ikusten duzuenez, hiru helburuak ezinbestekoak dira. Hala ere, badakigu asmo handiko helburuak direla, batez ere matematikaren bideari ekin berri dioten ikasleen bidelagun garenean.
Artikulu honetan, beraz, matematikaren ikaskuntzari nola heldu aztertuko dugu, arintasuna lortzeko.
Ulertu aplikatu aurretik, ala aplikatu ulertu aurretik?
Peter Liljedahlek, Diseñando aulas para pensar en matemáticas liburuan, 14 praktika proposatzen ditu ikasleen parte-hartzea sustatzeko eta pentsa dezaten lortzeko. Praktika horiek benetako protagonistak ikasleak izango diren gelak sortzera bideratuta daude, ikasleak errepikapen mekanikotik harago joan daitezen.
Zergatik bultzatu beharko genuke ikasleak matematikan mekanikoki aritzea, makina bat azkarrago eta hobeto arituko bada? Aldiz, ikasle batek ulertzen badu kentzeak zer esan nahi duen edo zergatik erabiltzen ditugun estrategia jakin batzuk (adibidez, zenbakien lerroan saltoak egitea), oinarri sendoagoa izango du kontzeptu berriak ikasteko.
Hala ere, arreta ulermenean jartzeak ez du esan nahi ez dituztenik eragiketak zuzen ebatzi behar. Emaitza zuzenera iritsi behar dute. Horregatik, ikasgelan praktikari ere denbora eskaintzen zaio, ikaskuntza sendotzeko eta arintasuna irabazteko.

Testuinguru horretan, ezinbestekoa da irakasleak gidari gisa duen eginkizuna. Irakasleak estrategiak modu argi eta gardenean aurkitzen lagundu behar du. Eta, ondoren, ikasleek praktikaren bidez edukiak sendotzen jarraitzen dutela ziurtatu behar du, konfort-zonatik irtetera animatuz eta apurka-apurka erronken eta prozeduren zailtasuna areagotuz.
Adibidez, ikasle batek kenketa batzuk ondo ebatzi baditu (ikasle bakoitzaren arabera) manipulatzeko materiala erabiliz, material hori gabe lan egitera animatzeko unea da, baina ikusizko irudikapenak erabiliko ditugu. Ikuspegi berri horrekin eragiketa batzuk zuzen ebatzi ondoren, aldamio horiek kendu behar ditugu beste behin, eta adierazpen-aldaketa gero eta abstraktuagoetara pasa. Eta horrela behin eta berriz.
Laguntza edo aldamio horiek funtsezkoak dira ikaskuntzaren lehen faseetan. Baina pixkanaka-pixkanaka desagertu behar dute, ikasleak pentsamendu abstraktuagoa lor dezan eta arintasuna lortzen joan dadin. Helburua ibilbidea osatzea da eragiketak inolako laguntzarik gabe ebatzi arte. Baina, hori bai, behar izanez gero, erabil ditzakeen estrategiak edukiko ditu.
KAA ereduan oinarritutako estrategien eraikuntza
Estrategia bakoitzak ulermenean oinarritutako ikaskuntza-sekuentzia zehatz bati jarraitzen dio: zer egiten ari garen.
Horregatik, KAA eredua (konkretua, adierazgarria, abstraktua) erabiltzen dugu: hiru etapa progresibotan oinarritzen den ikaskuntza matematikoko metodologia da, ikasleei kontzeptu matematikoak ulertzen eta menderatzen laguntzen diena.
Lehenik eta behin, hainbat material (konkretua) erabiliko ditugu manipulatzeko; jarraian, manipulatuz egiten genuena paperean adieraziko dugu (adierazgarria); eta, azkenik, adierazpen abstraktuetara igaroko gara, hala nola algoritmoak (abstraktua).
Zer da arintasuna?
Ikerketen arabera, arintasuna zenbakiekin, eragiketekin eta prozedurekin erraztasunez lan egiteko gaitasuna da.
Jariotasunak hiru sakontasun-maila ditu:
Arintasun faktikoa (fact fluency): memorizazioari edo automatizazioari esker, gertaera ezagunak edo ondorioztatutako gertaerak erraz gogoratzeko gaitasuna da. Esparru horren barruan sartzen dira digitu bateko batuketen automatizazioa, Lehen Hezkuntzako 1. eta 2. mailetan (7 + 3 = 10; 6 + 4 = 10; 8 + 7 = 15), eta digitu bateko biderketen automatizazioa (biderkatzeko taulak) Lehen Hezkuntzako 3. eta 4. mailetan.
Arintasun konputazionala (computational fluency): eragiketa sinpleetatik harago, eragiketak (konputatzea) erraztasunez egiteko gaitasuna da. Esparru horretan funtsezko gaitasunak sartzen dira, adibidez, saltoen estrategia edo zatiketaren banaketa-eredua behar bezala egitea.
Prozedura-arintasuna (procedural fluency): etapa bakoitzaren mende dauden eta oinarrizko eragiketa batetik harago doazen prozedurak erraztasunez jarraitzeko gaitasuna da. Esaterako, m.k.t. aurkitzea, eragiketa konbinatuak eta ekuazioak ebaztea, etab.
Gainera, arintasunaren definizioaren barruan, funtsezko hiru osagai eta sei ekintza daude:
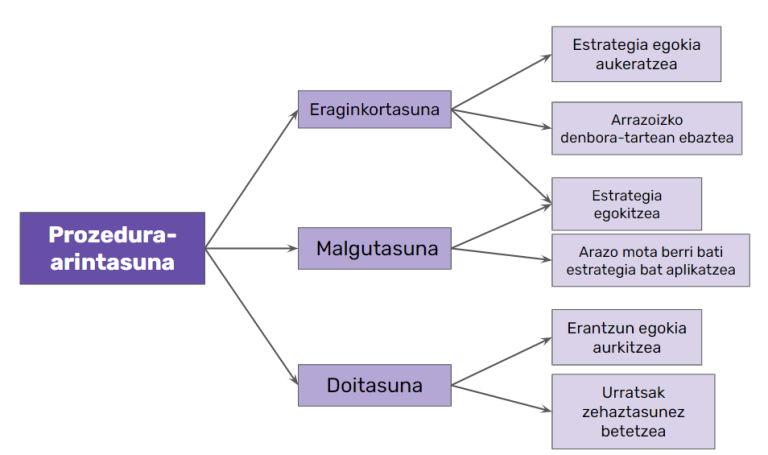
Ikusten duzuenez, arintasuna ez da eragiketak azkar egitea bakarrik. Era berean, eraginkorra eta malgua izan behar da estrategia bat aukeratzeko, testuinguruaren arabera egokitzeko eta emaitza zuzenera iristeko, urratsak behar bezala eginez.
Zer zeregini erantzun behar zaie azkar?
Askotan, ezagutzak ondo ulertu eta barneratzean oinarritzen den ikaskuntzaz hitz egiten dugunean, badirudi erantzunaren abiadura erabat deabrutzen dugula, baina ikasleen ezagutza automatikoaren parte izan beharko luketen hainbat eduki daude:
- Zifra bakarreko batuketen automatizazioa (0-10 tartea)
- Zifra bakarreko biderketen automatizazioa (biderkatzeko taulak)
Izan ere, arintasun faktikoaren esparruan sartzen diren edukietako batzuk dira. Ikasleek ez badakite azkar erantzuten eta ez badute emaitzak ondorioztatzeko estrategia eraginkorrik, esfortzua egin beharko dute oinarrizko kalkuluak egiteko, eta horrek murriztu egiten du alderdi aurreratuagoetan edo konplexuagoetan kontzentratzeko gaitasuna.
Horregatik, garrantzitsua da azkar erantzuten jakitea, dela emaitza buruz dakigulako, dela oso azkar ondorioztatu dugulako beste emaitza batzuetan oinarrituz, ahalegin handirik egin gabe. Adibidez, ikasle batek oso azkar ondoriozta dezake 60 + 70 = 130 dela 6 + 7 = 13 eragiketan oinarritzen bada.
Nola lortu eraginkorrak eta malguak izatea hainbat estrategia eraikiz
Ikusi dugunez, arintasuna garatzeko oinarrietako bat eragiketak egiteko modu desberdinak ezagutzea da. Hau da, ezinbestekoa da edozein eragiketa ebazteko aukera emango diguten estrategiak menderatzea, testuinguruaren eta eragiketako zenbaki moten arabera. Laburbilduz, malguak izan behar dugu.
Errepara diezaiegun batuketei eta kenketei, adibidez. Batzuetan, komeni da idatzizko algoritmoa erabiltzea. Beste batzuetan, nahiago dugu buruz kalkulatu, zenbakien lerroan saltoak imajinatuz. Halaber, emaitzak ondorioztatzeko gertaera ezagunetara jo dezakegu. Edo kalkulagailua erabil genezake.
Aukera ugari ditugula jakiteak eta horietatik egokiena aukeratzeak malgutasuna emango digu kalkulatzerakoan, eta eraginkorragoak izango gara. Hala ere, arintasuna lortzeko gakoa praktikatzea da.
Oinarrizko eragiketen ikaskuntza esanguratsua
Matematikaren ikaskuntza (batez ere zenbakikuntzaren atala) zientzia hierarkiko bat da: beharrezkoa da eduki bat barneratzea hurrengora igarotzeko. Oinarrizko eragiketak (batuketa, kenketa, biderketa eta zatiketa) funtsezkoak dira prozesu horretan, bidea urratzen baitute zenbakikuntza eta aljebrako beste kontzeptu aurreratuago batzuk ereiteko.
Algoritmoetatik harago, oinarrizko eragiketa bakoitza menderatzeak esan nahi du haren esanahia ulertzen dugula , eta badakigula nola ebazten den eta zer estrategia erabil ditzakegun hori lortzeko.
Eragiketa bakoitza iceberg bat bezalakoa da: gainazalean ikusten duguna konplexutasun osoaren zati txiki bat baino ez da. Urpean mantentzen den guztia eragiketa bakoitza menderatzeko eta zentzuz egiteko euskarria da.
Hori dela eta, baliabide hau sortu dugu. Liburutxo honek modu sintetiko eta bisualean laburbiltzen du oinarrizko eragiketa bakoitzaren ikaskuntzaren atzean ezkutatzen den guztia:
- Zer esan nahi duen batzeak, kentzeak, biderkatzeak eta zatitzeak.
- Zer estrategia proposatzen diren eragiketa bakoitza ebazteko.
- KAA ereduan oinarrituz, zer ikaskuntza-sekuentziari jarraitzen dion estrategia bakoitzak.
Ezagutza hori edukitzeak malguagoak eta eraginkorragoak izaten lagunduko digu. Dena den, praktikatzea funtsezkoa izango da kalkuluak azkarrago egiteko, baina alderdi hori aurrerago landuko dugu.
Oraingoz, baliabide honetan murgiltzera animatzen zaitugu, eragiketa bakoitza pentsatzeko, ulertzeko eta aurrera egiteko aukera bat izan dadin.
Deskargatu liburu elektronikoa
Ezagutu baliabide hau, oinarrizko eragiketetan gehien erabiltzen diren estrategiak modu bisualean laburbiltzen dituena.

Erreferentzia bibliografikoak:
- Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22-31.
- Bay-Williams, J. M., y SanGiovanni, J. J. (2021). Figuring out fluency: Mathematics teaching and learning, grades K-8: Moving beyond basic facts and memorization (1st ed.). Corwin.
- Hmelo‐Silver, C. E., Duncan, R. G., y Chinn, C. A. (2007). Scaffolding achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 99–107. https://doi.org/10.1080/0046150701263368
- Van den Heuvel-Panhuizen, M. (2008). Children learn mathematics: Learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Dutch design in mathematics education, V: 1. Utrecht: Freudenthal Institute, Sense Publishers.







