Haurren heltze-prozesu arrunta ezagutzea ezinbestekoa da bilakaera egokia bermatzeko. Adibidez, pediatrarenera eramaten ditugu haien altuera edo pisua adinerako espero dena den jakiteko. Bertan, medikuak haurraren balioak dagokion eskualdeko normaltasun-kurbekin konparatzen ditu (adibidea 1. irudian), eta dagozkion erabaki medikoak hartzen.
1. irudia. Altuera eta pisuaren kurbak 2 eta 20 urte bitarteko gizonezkoetan.
Halako prozesu analitikoak funtsezkoak dira hezkuntzaren alorrean ere, ikasleen bilakaerari buruzko informazio objektiboa beharrezkoa baita desorekarik agertuz gero dagozkion hezkuntza-erabakiak hartu ahal izateko.
Analisia eta ikerketaren emaitzak
Iazko ikasturte amaieran, Innovamaten ikerketa bat egin genuen, hain zuzen, haurrek alderdi matematiko jakinetan izandako bilakaerari buruzko informazio objektiboa lortzeko helburuarekin: errendimendu matematikoko kurben ikerketa (A999 ere deitua). Kasu hartan, gure ikerketa-aldagaia arintasun aritmetiko gehigarria izan zen, hau da, haurrak denbora jakin batean (gure proban, 2 minutu) egiteko gai diren tarte txikietako batuketa eta kenketa kopurua.
Horrela, arintasun hori neurtuko zuen jarduera digital bat sortu genuen Innovamat App-erako, eta, ikasturte amaieran, Innovamat egiten zuten HHko 5. mailatik LHko 6. mailara arteko 85.000 bat haurrek egin zuten (0-10 tarteko batuketak HHko 5. mailako eta LHko 1. mailako haurren kasuan, eta 0-10 tarteko batuketa eta kenketak, nahasian, LHko 2. mailatik aurrerakoen kasuan).
2. irudian ikus ditzakezue emaitzak, eta bertatik informazio asko atera dezakegu.
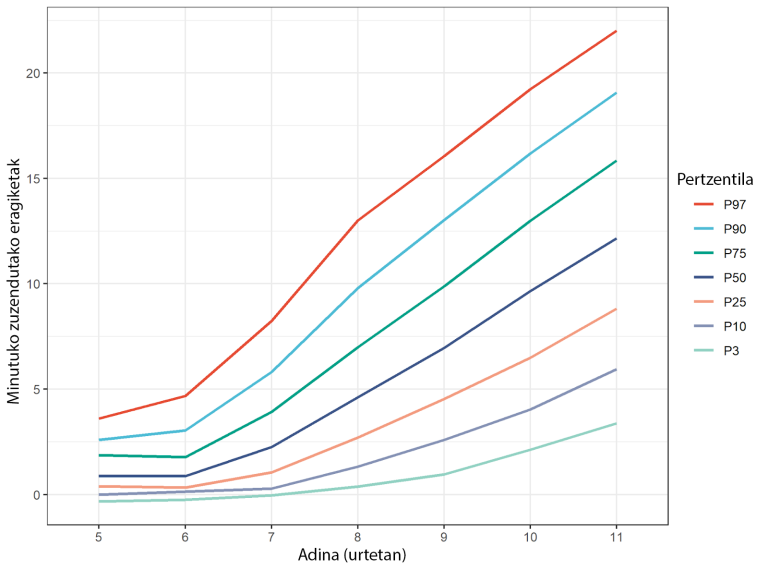
Alde batetik, Innovamaten, orain ikasleen bilakaeraren jarraipena egin dezakegu alderdi horri dagokionez, eta irakasleei laguntza hobea eskain diezaiekegu hezkuntza-erabakiak hartzerakoan, hala behar izanez gero.
Bestalde, beste efektu interesgarri batzuk ere ikus ditzakegu. Adibidez, banaketen zabalera (hau da, pertzentil baxuenaren eta altuenaren arteko distantzia) askoz txikiagoa da lehen mailetan azkenekoetan baino. Horrek erakusten digu errendimendu baxua duten haurrek, maila baxuagoa izateaz gain, motelago ikasteko joera dutela, eta, beraz, hasieran diferentzia txikiak zirenak handi bilakatzen dira amaieran, eta zailtasun horiek ez gainditzeko arriskua dago.
3. irudian beste datu garrantzitsu bat ikus dezakegu, teorikoki jada ezagutzen dena, baina enpirikoki hautematea zaila dena, behaketa-saio kopuru oso handia eskatzen baitu. Irudian adierazten den moduan, lehen mailetako banaketan “koskor” batzuk daude, eta, haurrek adinean gora egin ahala eta eskolan denbora gehiago eman ahala, desagertzeko joera dute, eta adin nagusikoetan estatistikoki banaketa normala lortzen da.
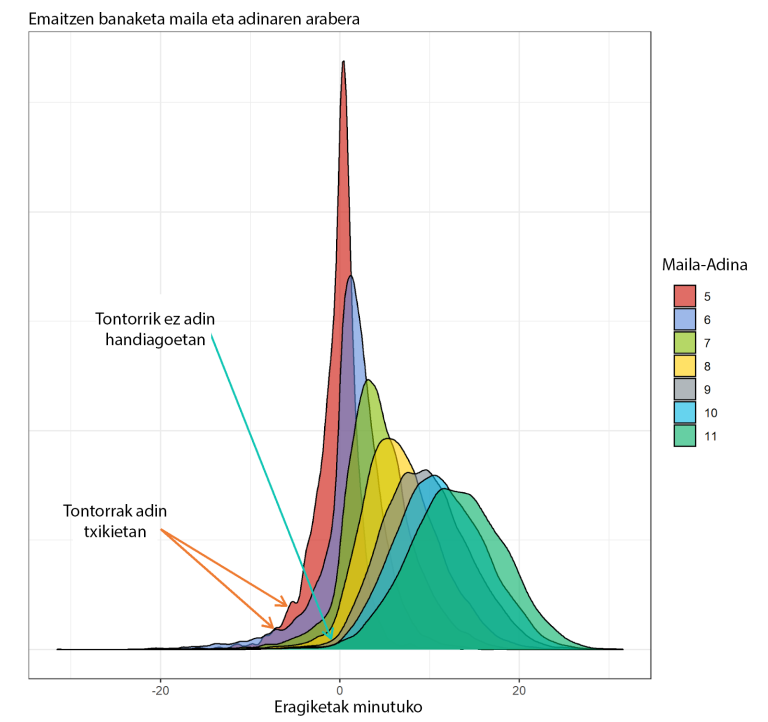
Hortik bi gauza ondoriozta ditzakegu: lehenengoa, HHko 5. edo LHko 1. mailara matematikaren ikaskuntza ez-formal oso eskasa duten ikasleak heltzen direla (normalean familiak ematen die ikaskuntza hori, eskolatu ez badira) eta, hortaz, espero litzatekeena baino kopuru handiagoa ikusten dugu oso pertzentil baxuan.
Efektu hori hezkuntza formalak zuzentzen duen neurria, ikusten dugu banaketa gero eta normalagoa dela (adibidez, Gaussen kanpai bat osatzen du). Hortik, ondorio oso garrantzitsua atera dezakegu: diskalkulia (beste artikulu honetan mintzo gara horretaz) ez da “dena ala ezer ez” erako fenomenoa (gripea izatea edo haurdun egotea bezala), banaketa normal baten isatsa baizik (esaterako, hipertentsioa edo hiperkolesterolemia). Aurkikuntza hori duela 30 urte egin zen dislexiarako (Shaywitz, S. E. et al., 1992), baina, dakigunez, oraindik ez da frogatu diskalkuliarako. Ikerketa honi eta etorriko direnei esker, ekarpenak egin ahal izatea espero dugu.
Shaywitz, S. E., Escobar, M. D., Shaywitz, B. A., Fletcher, J. M., & Makuch, R. (1992). Evidence that dyslexia may represent the lower tail of a normal distribution of reading ability. New England Journal of Medicine, 326(3), 145-150.






