Si queréis saber qué son y cómo proponemos gestionar estas tareas, podéis consultar este enlace.
Contenidos más relevantes: Numeración y cálculo, números, sumas, restas, regularidades.
Idea original: http://www.cut-the-knot.org/Curriculum/Games/ProizvolovGame.shtml
I. ¡Planteemos y empecemos a pensar!
¿Qué habéis descubierto?
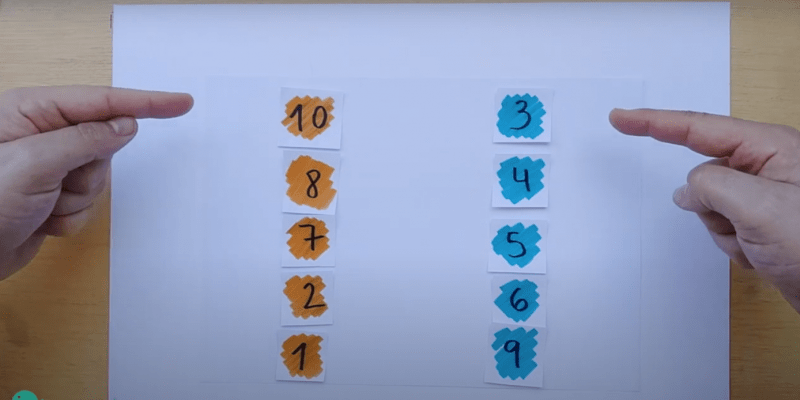
Pretendemos que el alumnado haga varias pruebas e investigue los resultados mientras ordenan, restan y suman, en busca de patrones
II. ¡Comprobemos y sigamos pensando!
Y con los números del 1 al 12, ¿qué observáis?
Pretendemos que el alumnado, después de hacer varias pruebas, analizar, comparar y razonar, se dé cuenta como mínimo de la regularidad en el resultado de la suma, que siempre es 25. No pretendemos que descubran por qué ni que lo justifiquen, aunque puede resultar interesante de ver con algunos alumnos y alumnas. Siempre da 25 porque, independientemente del orden en el que pongamos los números, la suma final siempre es:
10 + 9 + 8 + 7 + 6 – 5 – 4 – 3 – 2 – 1 =
= (10 – 3) + (8 – 4) + (7 – 5) + (6 – 2) + (9 – 1) =
= (10 – 5) + (9 – 4) + (8 – 3) + (7 – 2) + (6 – 1) =
= 5 + 5 + 5 + 5 + 5 = 5 x 5 = 25
Además, el alumnado deberá razonar para descubrir cómo afecta el cambio en las condiciones del enunciado a las soluciones que habían encontrado hasta ahora. En el vídeo, proponemos qué pasará con los números del 1 al 12, pero se pueden elegir otros rangos.
III. ¡Reflexionemos y vayamos más allá!
Pretendemos que el alumnado descubra que a pesar de cambiar el rango del 1 al 12, la suma también se mantiene constante. Esta vez, siempre da 36 porque, independientemente del orden en el que pongamos los números, la suma final siempre es:
12 + 11 + 10 + 9 + 8 + 7 – 6 – 5 – 4 – 3 – 2 – 1 = 6 x 6 = 36
¿Y con otros rangos? Por ejemplo, si lo hacemos con números entre 1 y 2n, siempre da n2. O si lo hacemos con números entre x y x + 2n – 1 también, siempre da n2. Por último, es interesante reflexionar que, para que el problema se pueda resolver, la cantidad de números debe ser par. Por ejemplo, en el vídeo se propone de hacer entre 3 y 11 pero, como esto son 9 números, no se puede. Si los niños nos lo dicen, entonces les podemos pedir como cambiarían el enunciado para poder hacerlo (añadiendo o quitando un número), y que lo intenten.