Conocer el proceso madurativo normal de los niños es fundamental para asegurar una correcta evolución. Por ejemplo, los llevamos al pediatra para saber si su altura o su peso son los esperados para su edad. Allí, el médico compara los valores del niño con las curvas de normalidad de su región (ejemplo en la Figura 1) y toma las decisiones médicas correspondientes.
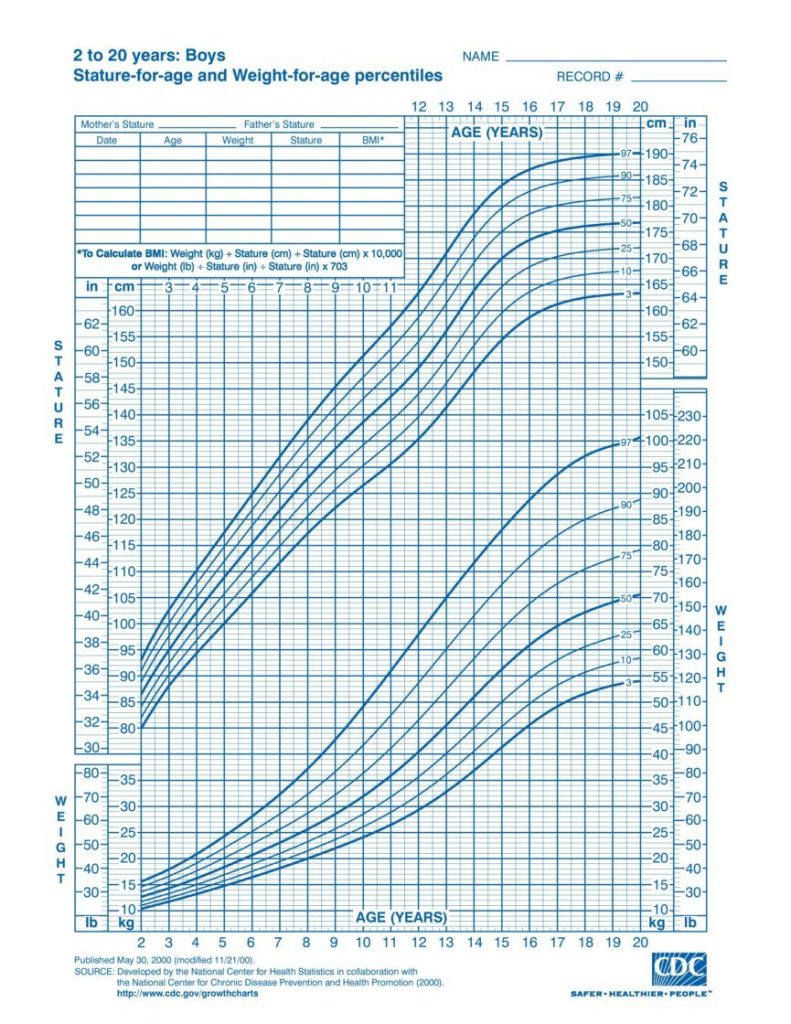
Figura 1. Curvas de estatura y peso en varones de 2 a 20 años.
Este proceso analítico también es crucial en educación, puesto que necesitamos información objetiva sobre la evolución de los alumnos para tomar las decisiones educativas pertinentes en caso de que haya desajustes.
Análisis y resultados del estudio
A finales del curso pasado, en Innovamat llevamos a cabo un estudio para tener, justamente, información objetiva sobre la evolución de los niños en aspectos matemáticos concretos, el estudio de curvas de rendimiento matemático (también llamado A999). Nuestra variable de estudio, en este caso, era la fluidez aritmética aditiva, es decir, la cantidad de sumas y restas en rangos pequeños que los niños son capaces de hacer en un tiempo concreto (2 minutos, en nuestra prueba).
Así pues, creamos una actividad digital para la App Innovamat que mide esta fluidez, e hicimos que la realizaran unos 85 000 niños de Innovamat desde Infantil 5 hasta 6º de primaria, a final de curso (sumas en el rango 0-10 para los niños de Infantil 5 y 1º de primaria, y sumas y restas mezcladas en el rango 0-20 a partir de 2º de primaria).
En la Figura 2 podéis ver las curvas resultantes, de las cuales podemos sacar mucha información.
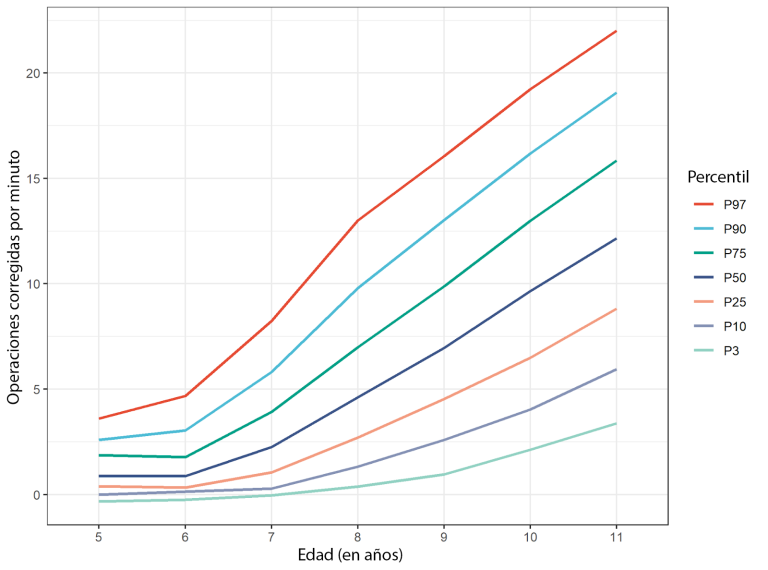
Por un lado, internamente desde Innovamat, ahora somos capaces de monitorizar la evolución de los alumnos en este aspecto y ayudar mejor a los maestros a tomar las decisiones educativas pertinentes, en caso de necesidad.
Por otro lado, también vemos otros efectos interesantes. Por ejemplo, la anchura de las distribuciones (es decir, la distancia entre los percentiles menores y los mayores) es mucho menor en cursos iniciales que en finales. Esto nos muestra que los niños con un rendimiento bajo no solo tienen un nivel más bajo, sino que también tienden a aprender más lentamente, por eso unas diferencias relativamente pequeñas al inicio se amplían a diferencias que tienen el riesgo de ser insalvables al final de la escuela primaria.
En la Figura 3 podemos ver otro hecho relevante, ya conocido de forma teórica, pero que es difícil de percibir de forma empírica porque requiere un número muy alto de observaciones. Tal como se indica en la Figura, hay unos «chichones» en las distribuciones de los primeros cursos que tienden a desaparecer a medida que los niños crecen y llevan más tiempos escolarizados, incluso resultante en una distribución estadísticamente normal en edades más grandes.
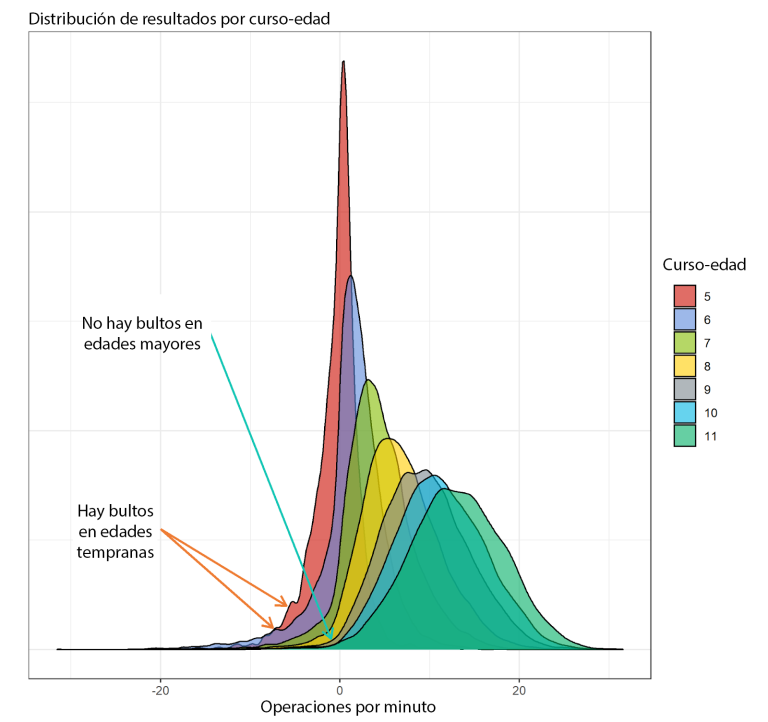
De aquí podemos inferir dos cosas: la primera es que hay alumnos que llegan a Infantil 5 o a 1º de primaria con un aprendizaje no formal de las matemáticas muy deficiente (habitualmente proporcionado por la familia, si no han sido escolarizados) y, por lo tanto, vemos una cantidad mayor de la que sería esperable en un percentil muy bajo.
A medida que este efecto es corregido por la educación formal, lo que vemos es que la distribución es cada vez más normal (p. ej., forma una campana de Gauss). De esto podemos inferir una conclusión muy relevante: la discalculia (de la que hablamos en este otro artículo) no es un fenómeno de «todo o nada» (como tener la gripe o estar embarazada), sino que es la cola de una distribución normal (como la hipertensión o la hipercolesterolemia). Este es un hecho que se descubrió hace 30 años para la dislexia (Shaywitz, S. E. et al., 1992), pero, por lo que sabemos, todavía no se ha demostrado para la discalculia. Gracias al presente estudio y a los que lo seguirán, esperamos poder contribuir.
Shaywitz, S. E., Escobar, M. D., Shaywitz, B. A., Fletcher, J. M., & Makuch, R. (1992). Evidence that dyslexia may represent the lower tail of a normal distribution of reading ability. New England Journal of Medicine, 326(3), 145-150.






