Baixe o e-book
Descubra este recurso que sintetiza de forma visual algumas das estratégias mais utilizadas nas operações básicas.

Artigos relacionados:
- A adição (em breve)
- A subtração (em breve)
- A multiplicação (em breve)
- A divisão (em breve)
Sabemos que a matemática não se resume às operações, porém… o que é mais importante ao aprender esta parte fundamental da matemática? Compreender o que estamos fazendo? Chegar ao resultado correto? Ou resolver as operações em um prazo razoável?
Como professores, temos altas expectativas de aprendizagem em relação aos nossos alunos. E devemos ser ambiciosos!
- Os alunos devem compreender o que estão fazendo e o por quê de fazê-lo.
- Eles têm que chegar ao resultado correto aplicando os procedimentos corretamente.
- E também devem resolver as operações de forma eficiente em um prazo razoável.
Como você pode ver, não há apenas uma resposta correta: os três objetivos são essenciais. Porém, sabemos que esta é uma meta ambiciosa. Principalmente quando estamos diante de uma turma que está apenas no início da sua trajetória pela matemática.
Por isso, exploramos, neste artigo, formas de abordar o ensino da matemática para alcançar a fluência.
Entender antes de aplicar ou aplicar antes de entender?
No livro Projetando salas de aula para pensar sobre matemática, Peter Liljedahl propõe 14 práticas para promover a participação dos alunos na sala de aula e incentivá-los a pensar. Estas práticas visam a criar aulas nas quais os alunos sejam os verdadeiros protagonistas, estimulando-os a ir mais além da simples repetição mecânica.
Por que encorajaríamos os alunos apenas a executar mecanicamente operações que uma máquina poderia fazer melhor e mais rápido? Por outro lado, quando um aluno entende conceitos como o que significa subtrair, ou por que usamos determinadas estratégias, como saltar na linha numérica, ele obtém uma base mais sólida para novos aprendizados.
É claro que focar no entendimento não significa que eles seja desnecessário resolver as operações corretamente. Claro que os alunos devem chegar ao resultado correto. É por isso que também dedicamos tempo à prática na sala de aula, para consolidar o aprendizado e ganhar fluência.

Dentro deste contexto, é indispensável o papel do professor como guia. Ele deve ajudar os alunos a descobrirem as estratégias de forma clara e transparente. E depois, fazer com que consolidem o conteúdo por meio da prática, incentivando-os a sair da zona de conforto e aumentando gradativamente a dificuldade dos desafios e procedimentos.
Por exemplo, se um aluno resolveu corretamente algumas subtrações utilizando material manipulável, é recomendado convidá-lo a trabalhar sem o material, utilizando apenas as representações visuais. Quando ele tiver resolvido corretamente mais algumas operações com essa nova abordagem, retiramos novamente os “andaimes” e o ajudamos na transição a uma representação mais abstrata. E assim por diante.
Esses apoios, ou “andaimes”, são essenciais nas primeiras fases da aprendizagem. Mas eles devem desaparecer gradativamente, para que o aluno alcance um pensamento mais abstrato e ganhe fluência. O objetivo é completar o percurso que leva à resolução das operações sem qualquer tipo de apoio. Tudo o que ele deve precisar são estratégias às quais recorrer se necessário.
Construção de estratégias baseadas no modelo CPA
Cada estratégia segue uma sequência de aprendizagem específica que se baseia na compreensão do que estamos fazendo.
É por isso que seguimos o modelo CPA (concreto, pictórico, abstrato), uma metodologia de aprendizagem matemática baseada em três etapas progressivas que ajudam os alunos a compreender e dominar os conceitos matemáticos.
Primeiro, partimos da manipulação de diversos materiais (o concreto). Em seguida, representamos no papel o que fizemos de forma manipulativa (o pictórica). E, por fim, passamos para as representações simbólicas, como os algoritmos (o abstrato).
O que entendemos por fluência?
As pesquisas definem fluência como a capacidade de trabalhar com desenvoltura com números, operações e procedimentos.
A fluência tem três níveis de profundidade:
Fluência factual (fact fluency): capacidade de recordar fatos conhecidos ou derivados com facilidade graças à automatização. Neste nível, se enquadra a automatização da adição de um dígito, no 1.º e 2.º anos (7 + 3 = 10; 6 + 4 = 10; 8 + 7 = 15), e a automatização das multiplicações de um dígito (tabuadas de multiplicação), no 3º e 4º anos do Ensino Fundamental.
Fluência computacional (computational fluency): capacidade de realizar operações (computar) com desenvoltura, mais além das operações básicas. Neste nível, estão habilidades essenciais que vão desde a execução correta da estratégia dos saltos até o modelo de distribuição da divisão.
Fluência procedimental (procedural fluency): capacidade de seguir com desenvoltura procedimentos que vão além de uma operação básica e que dependem de cada etapa. Aqui, estamos nos referindo a coisas como encontrar o mcm, resolver operações combinadas, equações, etc.
Além disso, dentro da definição de fluência, há três componentes principais e seis ações relacionadas:
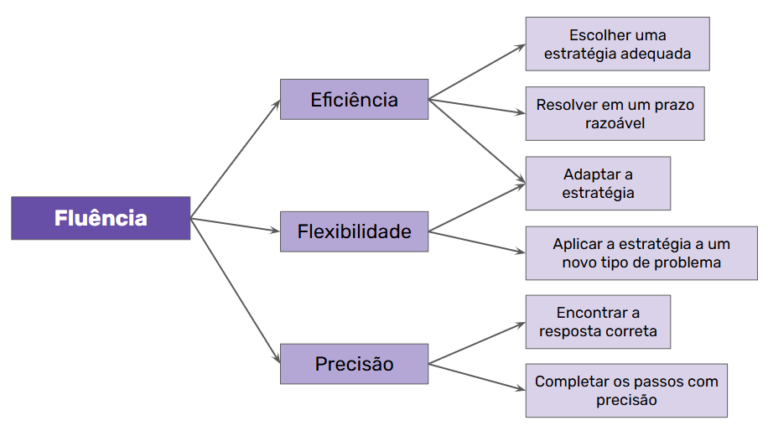
Como você pode perceber, ter fluência não é apenas resolver operações rapidamente. Significa também ser eficiente e flexível ao escolher uma estratégia, adaptá-la ao contexto e chegando ao resultado correto, completando as etapas com precisão.
Que fatos devem ser respondidos rapidamente?
Muitas vezes, quando falamos em aprendizagem baseada na compreensão profunda do conhecimento, parece que estamos demonizando a velocidade de resposta, mas há vários conteúdos que devem fazer parte do conhecimento automático dos alunos. Eles são:
- As adições de um dígito (intervalo de 0 a 10)
- As multiplicações de um dígito (tabuadas de multiplicação)
De fato, eles são alguns dos conteúdos que se enquadram no nível da fluidez factual. Não saber responder rapidamente e, pior ainda, não ter estratégias eficientes para deduzir os resultados, são coisas que fazem com que os alunos tenham que dedicar esforços aos cálculos básicos, reduzindo sua capacidade de concentração em aspectos mais avançados ou complexos.
Por isso é importante saber responder rapidamente, seja porque sabemos de cor ou porque fizemos a dedução imediata a partir de alguns resultados básicos, sem muito esforço. Por exemplo, um aluno pode deduzir rapidamente que 60 + 70 = 130 se sabe que 6 + 7 = 13.
Como conseguir eficiência e flexibilidade por meio da construção de várias estratégias
Como vimos, um dos pilares para desenvolver a fluência é conhecer diferentes formas de lidar com as operações. Ou seja, dominar diversas estratégias que nos permitem resolver qualquer operação dependendo do contexto e dos números envolvidos. Resumindo, ter flexibilidade.
Vamos observar a adição e a subtração, por exemplo. Às vezes, é conveniente usar o algoritmo escrito. Outras vezes, é preferível fazer um cálculo mental imaginando saltos na linha numérica. Há momentos em que podemos deduzir o resultado de fatos que já conhecemos. E há outros em que simplesmente queremos usar uma calculadora.
Conhecer essa variedade (e saber escolher) é o que nos torna flexíveis e eficientes na hora de calcular. Porém, só com a prática poderemos ganhar agilidade na execução.
Aprendizagem significativa das operações básicas
A aprendizagem da matemática (principalmente no que diz respeito à numeração) possui uma estrutura hierárquica: é necessário pisar em um conteúdo para poder avançar para o próximo. As operações básicas (adição, subtração, multiplicação e divisão) são fundamentais neste processo, pois abrem caminho para semear outros conceitos mais avançados de numeração e/ou álgebra.
Mais além dos algoritmos, o domínio da operação básica envolve compreender o seu significado, saber como se resolve e quais estratégias podemos usar para isso.
Cada operação é como um iceberg: o que vemos na superfície é apenas uma pequena parte de toda a complexidade. O que fica submerso é também o que sustenta e dá sentido ao domínio de cada operação.
A partir disso, criamos este recurso. Trata-se de um livrinho que resume de forma sintética e visual tudo o que se esconde na aprendizagem de cada operação básica:
- O que significa somar, subtrair, multiplicar e dividir.
- Quais são as estratégias propostas para resolver cada operação.
- Qual é a sequência de aprendizagem de cada estratégia com base no modelo CPA.
Ter esses conhecimentos nos permitirá ser mais flexíveis e eficientes. Por outro lado, a prática será fundamental para ganhar velocidade nos cálculos, que é um aspecto que trabalharemos mais adiante.
Por enquanto, convidamos você a mergulhar neste recurso e explorar suas profundezas para transformar o aprendizado de cada operação em uma oportunidade de pensar, compreender e progredir.
Baixe o e-book
Descubra este recurso que sintetiza de forma visual algumas das estratégias mais utilizadas nas operações básicas.

Referências bibliográficas
- Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22-31.
- Bay-Williams, J. M., y SanGiovanni, J. J. (2021). Figuring out fluency: Mathematics teaching and learning, grades K-8: Moving beyond basic facts and memorization (1st ed.). Corwin.
- Hmelo‐Silver, C. E., Duncan, R. G., y Chinn, C. A. (2007). Scaffolding achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 99–107. https://doi.org/10.1080/0046150701263368
- Van den Heuvel-Panhuizen, M. (2008). Children learn mathematics: Learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Dutch design in mathematics education, V: 1. Utrecht: Freudenthal Institute, Sense Publishers.







