Conoscere il normale processo di maturazione dei bambini è fondamentale per garantirne la corretta evoluzione. Ad esempio, li portiamo dal pediatra per sapere se i valori relativi alla loro altezza o al loro peso rientrano nei parametri dei bambini della stessa età. Il medico confronta i valori del bambino con le curve di normalità della sua regione (esempio nella Figura 1) e prende le decisioni mediche corrispondenti.
Figura 1. Curve di altezza e peso nei maschi di età compresa tra 2 e 20 anni.
Questo processo analitico è cruciale anche nell’istruzione, poiché, per prendere le decisioni educative pertinenti, abbiamo bisogno di informazioni obiettive sull’evoluzione degli alunni.
Analisi e risultati dello studio
Alla fine dello scorso anno scolastico, noi di Innovamat abbiamo condotto uno studio per ottenere informazioni precise e obiettive sull’evoluzione dei bambini relativamente ad aspetti matematici specifici: lo studio delle curve di rendimento matematico (chiamato anche A999). La nostra variabile di studio, in questo caso, era la fluidità aritmetica additiva, ovvero la quantità di addizioni e sottrazioni all’interno di piccoli intervalli che i bambini sono in grado di fare in un tempo specifico (2 minuti, nel nostro test).
Abbiamo quindi creato un’attività digitale per l’App Innovamat che misura questa fluidità e l’abbiamo fatta eseguire a circa 85.000 bambini che usano Innovamat, dall’ultimo anno di scuola dell’infanzia al primo anno di scuola secondaria di primo grado, alla fine dell’anno scolastico (addizioni nell’intervallo 0-10 per i bambini di scuola dell’infanzia e primo anno di scuola primaria, e addizioni e sottrazioni miste nell’intervallo 0-20 dal secondo anno di scuola primaria in poi).
Nella Figura 2 sono illustrate le curve risultanti, da cui è possibile ricavare molte informazioni.
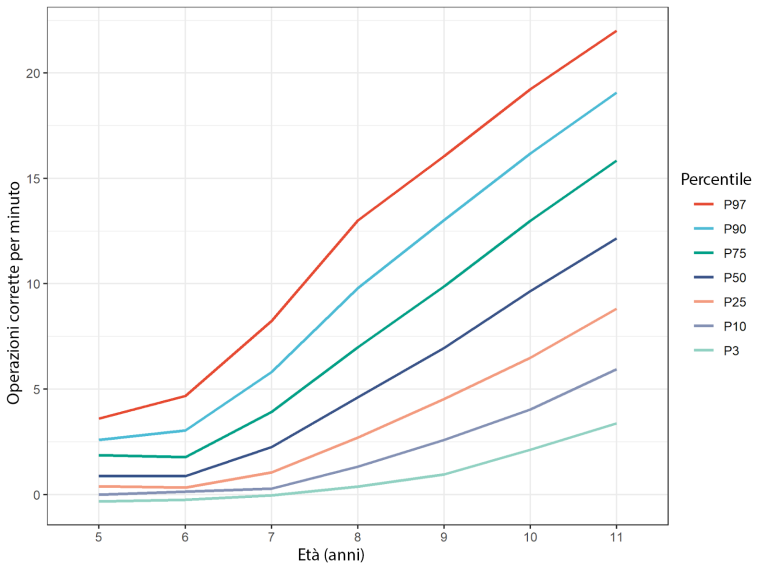
Da un lato, internamente (noi di Innovamat) ora siamo in grado di monitorare l’evoluzione degli alunni e di aiutare meglio gli insegnanti a prendere le decisioni educative pertinenti, se necessarie.
Dall’altro, notiamo anche altri effetti interessanti. Ad esempio, la larghezza delle distribuzioni (cioè la distanza tra il percentile più basso e quello più alto) è molto più piccola nei corsi iniziali rispetto a quelli finali. Questo dato dimostra che i bambini con scarso rendimento non solo hanno un livello più basso rispetto agli altri, ma tendono anche ad apprendere più lentamente, a tal punto che differenze relativamente piccole all’inizio si trasformano in differenze che rischiano di essere insormontabili alla fine del percorso di scuola primaria.
Nella figura 3 è possibile notare un altro fatto rilevante, già noto a livello teorico, ma che è difficile da percepire empiricamente perché richiede un numero molto elevato di osservazioni. Come indicato nella Figura, ci sono alcuni «dossi» nelle distribuzioni dei primi anni di scuola che tendono a scomparire con l’avanzare dell’età e della frequenza scolastica, fino ad arrivare a una distribuzione statisticamente normale nelle età più avanzate.
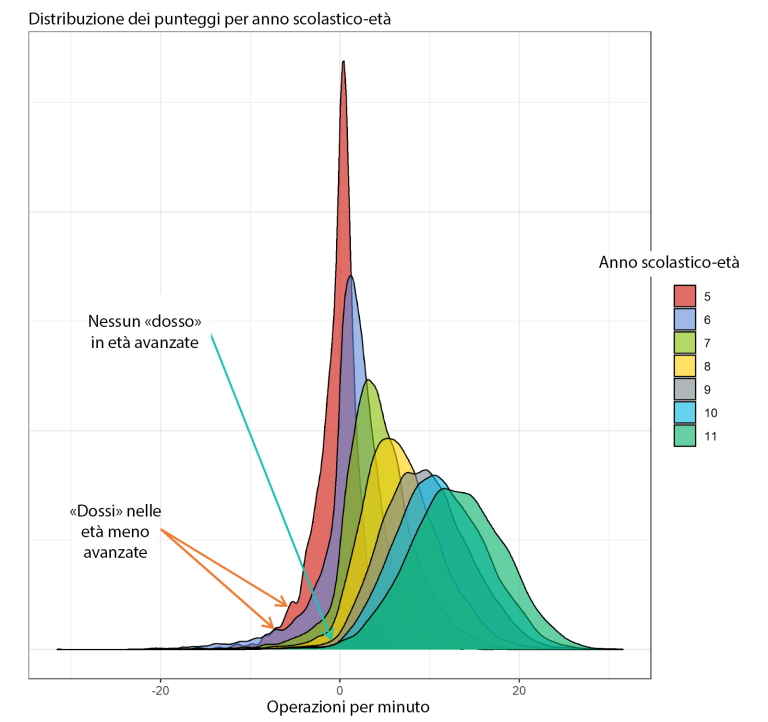
Da ciò si possono dedurre due cose: la prima è che ci sono alunni che arrivano all’ultimo anno di scuola dell’infanzia o al primo anno di scuola primaria con un apprendimento non formale della matematica molto scarso (di solito fornito dalla famiglia, se non sono stati scolarizzati) e, pertanto, notiamo una quantità maggiore di quanto ci si aspetterebbe in un percentile molto basso.
Correggendo questo effetto con l’istruzione formale, ciò che vediamo è che la distribuzione diventa sempre più normale (ad esempio, forma una campana gaussiana). Da ciò è possibile dedurre una conclusione molto rilevante: la discalculia (di cui parliamo in questo altro articolo) non è un fenomeno «tutto o niente» (come avere l’influenza o essere incinta), ma piuttosto è la coda di una distribuzione normale (come ipertensione o ipercolesterolemia). Si tratta di un fatto scoperto 30 anni fa per la dislessia (Shaywitz, S. E. et al., 1992), ma che, per quanto ne sappiamo, non è stato ancora dimostrato per la discalculia. Con questo studio e con quelli che condurremo in futuro, speriamo di poter, anche noi, dare il nostro contributo.
Shaywitz, S. E., Escobar, M. D., Shaywitz, B. A., Fletcher, J. M., & Makuch, R. (1992). Evidence that dyslexia may represent the lower tail of a normal distribution of reading ability. New England Journal of Medicine, 326(3), 145-150.






