Scarica l'e-book
Scopri questa risorsa che sintetizza in modo visivo alcune delle strategie più utilizzate nelle operazioni di base.

Articoli correlati:
- L’addizione (presto disponible)
- La sottrazione (presto disponible)
- La moltiplicazione (presto disponible)
- La divisione (presto disponible)
Inutile dire che fare matematica non si riduce al semplice calcolo delle operazioni. Ma cosa è più importante per l’apprendimento di questa parte fondamentale della matematica: capire cosa stiamo facendo, ottenere il risultato corretto o completare i calcoli in tempi ragionevoli?
Come insegnanti, è bene tenere alte le nostre aspettative sulle capacità di apprendimento degli alunni. Bisogna essere ambiziosi!
- Gli alunni devono comprendere ciò che stanno facendo e perché lo stanno facendo.
- Devono arrivare al risultato giusto applicando i procedimenti corretti.
- Devono risolvere le operazioni in modo efficiente e in un periodo di tempo ragionevole.
Questi tre obiettivi non si escludono a vicenda: sono tutti indispensabili e interconnessi. È vero, è una sfida ambiziosa. Soprattutto quando lavoriamo con alunni che hanno iniziato da poco il loro percorso di apprendimento della matematica.
In questo articolo, analizziamo come promuovere un apprendimento della matematica orientato allo sviluppo della fluidità.
Capire prima di applicare o applicare prima di capire?
Peter Liljedahl, nel suo libro Building Thinking Classrooms in Mathematics, propone 14 strategie per stimolare il coinvolgimento degli alunni e promuovere il pensiero matematico. Queste strategie mirano a creare aule in cui gli alunni si sentano i veri protagonisti, invitandoli ad andare oltre la semplice ripetizione meccanica di concetti e procedure.
Perché dovremmo promuovere la creazione di ambienti in cui gli alunni non fanno altro che eseguire meccanicamente ciò che potrebbe fare meglio e più velocemente una macchina? Quando un alunno comprende concetti come il significato della sottrazione o il motivo per cui è meglio utilizzare determinate strategie, come i salti sulla linea numerica, acquisisce una base più solida per continuare ad apprendere.
Concentrarsi sulla comprensione di procedure e concetti non significa togliere importanza all’ottenimento del risultato corretto. Sì, gli alunni devono ottenere il risultato corretto. E per farlo, è importante dedicare tempo alla pratica e permettere loro di consolidare l’apprendimento e acquisire fluidità.

In questo contesto, il ruolo dell’insegnante come guida è indispensabile. L’insegnante deve aiutare a scoprire le strategie in modo chiaro e trasparente e poi assicurarsi che gli alunni continuino a consolidare i contenuti attraverso la pratica, incoraggiandoli a uscire dalla loro zona di comfort e aumentando gradualmente la difficoltà delle sfide e dei procedimenti.
Per fare un esempio, se un alunno risolve correttamente alcune sottrazioni con l’aiuto del materiale manipolativo, lo spingiamo a mettere queste risorse da parte per iniziare a lavorare con rappresentazioni visive. Quando saprà risolvere correttamente le operazioni anche con questo nuovo strumento, lo accompagneremo lungo un percorso che prevede l’uso di rappresentazioni sempre più astratte.
Questo tipo di aiuti, o impalcature (dell’inglese scaffolding), sono essenziali nelle prime fasi dell’apprendimento, ma devono essere eliminati gradualmente, per permettere all’alunno di sviluppare un modo di ragionare sempre più astratto e acquisire fluidità. L’obiettivo è saper risolvere le operazioni senza alcun tipo di supporto, avendo delle strategie a cui ricorrere in caso di necessità.
Creazione di una strategia basata sul modello CRA
Ciascuna delle strategie fa riferimento a una sequenza di apprendimento specifica basata sulla comprensione e che si ispira al modello CRA (Concreto, Rappresentativo, Astratto), una metodologia di apprendimento matematico articolata in tre fasi progressive e pensata per aiutare gli alunni a comprendere e padroneggiare i concetti matematici.
Si inizia con la manipolazione di diversi materiali (fase concreta), si prosegue rappresentando su carta quanto fatto in modo manipolativo (fase rappresentativa) e infine si passa alle rappresentazioni astratte, ad esempio, all’uso di algoritmi (fase astratta).
Cos'è la fluidità?
La ricerca definisce la fluidità come la capacità di lavorare con numeri, operazioni e procedimenti con scioltezza.
La fluidità si sviluppa su tre livelli di profondità:
Fluidità fattuale (fact fluency): è la capacità di ricordare con facilità fatti noti o derivati attraverso la memorizzazione o l’automatizzazione. In questo contesto si inserisce l’automatizzazione delle addizioni con numeri di una cifra, nel 1° e 2° anno di Scuola primaria (7 + 3 = 10; 6 + 4 = 10; 8 + 7 = 15), e l’automatizzazione delle moltiplicazioni con numeri di una cifra (tabelline), nel 3° e 4° anno di Scuola primaria.
Fluidità computazionale (computational fluency): è la capacità di eseguire calcoli con fluidità, andando oltre le semplici operazioni di base. Questo concetto include alcune competenze chiave come la corretta esecuzione della strategia dei salti e l’applicazione del modello di distribuzione della divisione.
Fluidità procedurale (procedural fluency): consiste nella capacità di eseguire con scioltezza procedure che vanno oltre il calcolo di operazioni di base e si sviluppano in relazione alle diverse fasi dell’apprendimento. Questo include, ad esempio, la ricerca del minimo comune multiplo, la risoluzione di operazioni combinate, la soluzione di equazioni e altre competenze avanzate.
Inoltre, la definizione di fluidità comprende tre componenti chiave e sei azioni strettamente correlate:
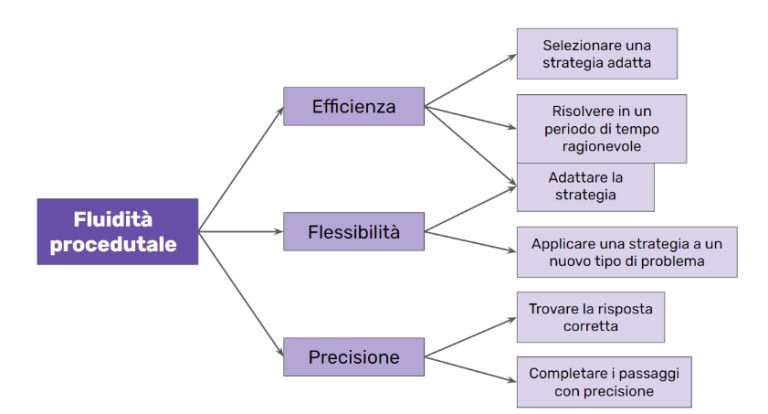
Quindi, acquisire fluidità non vuol dire solo riuscire a risolvere operazioni rapidamente. Significa anche essere efficienti e flessibili nella scelta delle strategie, saperle adattare al contesto e ottenere il risultato corretto completando i passaggi con precisione.
Quali conoscenze bisogna automatizzare?
Spesso, quando si parla di apprendimento basato sulla comprensione profonda della conoscenza, la velocità di risposta viene percepita come qualcosa di negativo. In realtà, esistono una serie di contenuti che gli alunni dovrebbero automatizzare. Vediamoli nel dettaglio:
- Automatizzazione delle addizioni con numeri di una cifra (intervallo 0-10)
- Automatizzazione delle moltiplicazioni con numeri di una cifra (tabelline)
Questi sono alcuni dei contenuti che rientrano nell’ambito della fluidità fattuale. Non saper rispondere rapidamente e non disporre di strategie efficaci per dedurre risultati significa dover affrontare calcoli di base, limitando la capacità di concentrarsi su aspetti più avanzati o complessi.
Saper rispondere rapidamente è importante, sia che ciò avvenga perché sappiamo qualcosa a memoria, sia che ciò derivi da deduzioni basate sull’osservazione di alcuni risultati di base. Ad esempio, uno alunno può velocemente dedurre che 60 + 70 = 130 sapendo che 6 + 7 = 13.
Come essere efficienti e flessibili nell'uso delle strategie
Come abbiamo visto, uno dei pilastri dello sviluppo della fluidità risiede nel disporre di diversi modi di affrontare le operazioni, ovvero nel padroneggiare diverse strategie che ci permettano di risolvere qualsiasi operazione a seconda del contesto e dei numeri coinvolti. In breve, la fluidità risiede nell’essere flessibili.
Facciamo l’esempio di addizioni e sottrazioni. A volte conviene utilizzare l’algoritmo scritto; altre volte, preferiamo fare un calcolo mentale immaginando salti sulla linea numerica; talvolta è possibile dedurre il risultato a partire da fatti che già conosciamo; infine, in alcune occasioni, è meglio utilizzare la calcolatrice.
Conoscere queste opzioni e saper scegliere lo strumento più adatto alla situazione o al problema è ciò che ci rende flessibili ed efficienti, mentre la pratica ci aiuta ad acquisire agilità nell’esecuzione dei calcoli.
Apprendimento significativo delle operazioni di base
L’apprendimento della matematica (soprattutto dei concetti di numerazione) ha una struttura gerarchica: è necessario esplorare un contenuto per passare a quello successivo. Le operazioni di base (addizione, sottrazione, moltiplicazione e divisione) sono fondamentali in questo processo, perché aprono la strada ai contenuti più avanzati di numerazione e/o algebra.
Al di là degli algoritmi, la padronanza di ogni operazione di base implica la comprensione del suo significato e delle strategie che possono essere utilizzate per risolverla.
Ogni operazione è come un iceberg: ciò che vediamo in superficie è solo una piccola parte della sua complessità. Tutto ciò che resta sott’acqua sostiene e dà significato all’operazione.
Abbiamo ideato un e-book che riassume in modo sintetico e visivo tutto ciò che si nasconde dietro l’apprendimento delle operazioni di base:
- Cosa significa sommare, sottrarre, moltiplicare e dividere.
- Quali strategie proponiamo per risolvere ogni operazione.
- A quale sequenza di apprendimento, basata sul modello CRA, fa riferimento ogni strategia.
Questa conoscenza ci permetterà di essere flessibili ed efficienti. Tuttavia, la pratica sarà essenziale per acquisire la velocità di calcolo, un aspetto su cui lavoreremo più avanti.
Per il momento, ti invitiamo a immergerti ed esplorare questa risorsa per trasformare l’apprendimento di ogni operazione in un’opportunità per pensare, capire e fare progressi.
Scarica l'e-book
Scopri questa risorsa che sintetizza in modo visivo alcune delle strategie più utilizzate nelle operazioni di base.

Riferimenti bibliografici:
- Baroody, A. J. (2006). Why children have difficulties mastering the basic number combinations and how to help them. Teaching Children Mathematics, 13(1), 22-31.
- Bay-Williams, J. M., y SanGiovanni, J. J. (2021). Figuring out fluency: Mathematics teaching and learning, grades K-8: Moving beyond basic facts and memorization (1st ed.). Corwin.
- Hmelo‐Silver, C. E., Duncan, R. G., y Chinn, C. A. (2007). Scaffolding achievement in problem-based and inquiry learning: A response to Kirschner, Sweller, and Clark (2006). Educational Psychologist, 42, 99–107. https://doi.org/10.1080/0046150701263368
- Van den Heuvel-Panhuizen, M. (2008). Children learn mathematics: Learning-teaching trajectory with intermediate attainment targets for calculation with whole numbers in primary school. Dutch design in mathematics education, V: 1. Utrecht: Freudenthal Institute, Sense Publishers.







