Conèixer el procés maduratiu normal dels infants és fonamental per assegurar-ne una correcta evolució. Per exemple, els portem al pediatre per saber si la seva alçada o pes són els esperats per a la seva edat. Allà, el metge compara els valors de l’infant amb les corbes de normalitat de la seva regió (exemple a la Figura 1) i pren les decisions mèdiques corresponents.
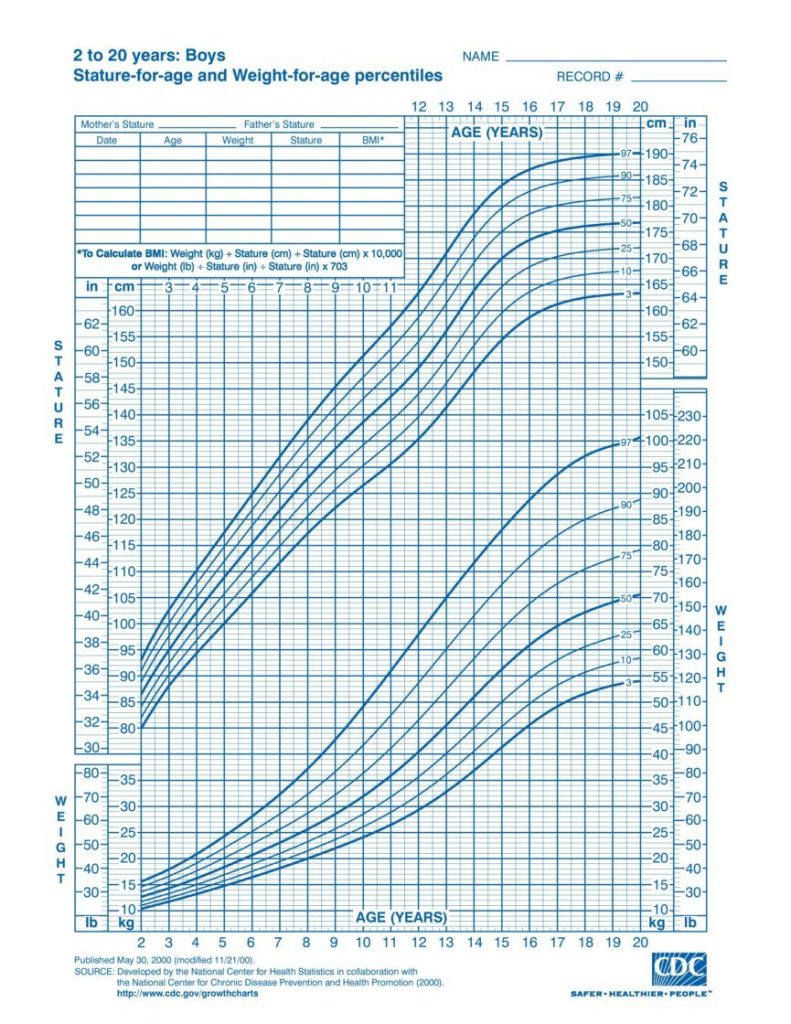
Aquest procés analític també és crucial en l’educació, ja que necessitem informació objectiva sobre l’evolució dels infants per prendre les decisions educatives pertinents en cas que hi hagi desajustos.
Anàlisi i resultats de l’estudi
A finals del curs passat, a Innovamat vam dur a terme un estudi per tenir, justament, informació objectiva sobre l’evolució dels infants en aspectes matemàtics concrets, l’estudi de corbes de rendiment matemàtic (també anomenat A999). La nostra variable d’estudi, en aquest cas, era la fluïdesa aritmètica additiva, és a dir, la quantitat de sumes i restes en rangs petits que els infants són capaços de fer en un temps concret (2 minuts, en la nostra prova).
Així doncs, vam crear una activitat digital per a l’App Innovamat que mesura aquesta fluïdesa, i la vam fer fer a uns 85 000 infants d’Innovamat des d’I5 fins a 6è de primària, a finals de curs (sumes en el rang 0-10 per als infants d’I5 i 1r, i sumes i restes barrejades en el rang 0-20 a partir de 2n).
A la Figura 2 podeu veure les corbes resultants, de les quals en podem treure molta informació.

D’una banda, internament des d’Innovamat, ara som capaços de monitorar l’evolució dels infants en aquest aspecte i ajudar més els mestres a prendre les decisions educatives pertinents, en cas de necessitat.
D’altra banda, però, també veiem altres efectes interessants. Per exemple, l’amplada de les distribucions (és a dir, la distància entre els percentils més petits i els més grans) és molt més petita en cursos inicials que en finals. Això ens mostra que els infants amb un rendiment baix no només tenen un nivell més baix, sinó que també tendeixen a aprendre més lentament, per això unes diferències relativament petites a l’inici s’amplien a diferències que tenen el risc de ser insalvables al final de l’escola primària.
A la Figura 3 podem veure un altre fet rellevant, ja conegut de forma teòrica, però que és difícil de percebre de forma empírica perquè requereix un nombre molt alt d’observacions. Tal com s’indica a la Figura, hi ha uns «bonys» en les distribucions dels primers cursos que tendeixen a desaparèixer a mesura que els nens creixen i porten més temps escolaritzats, àdhuc resultant en una distribució estadísticament normal a edats més grans.
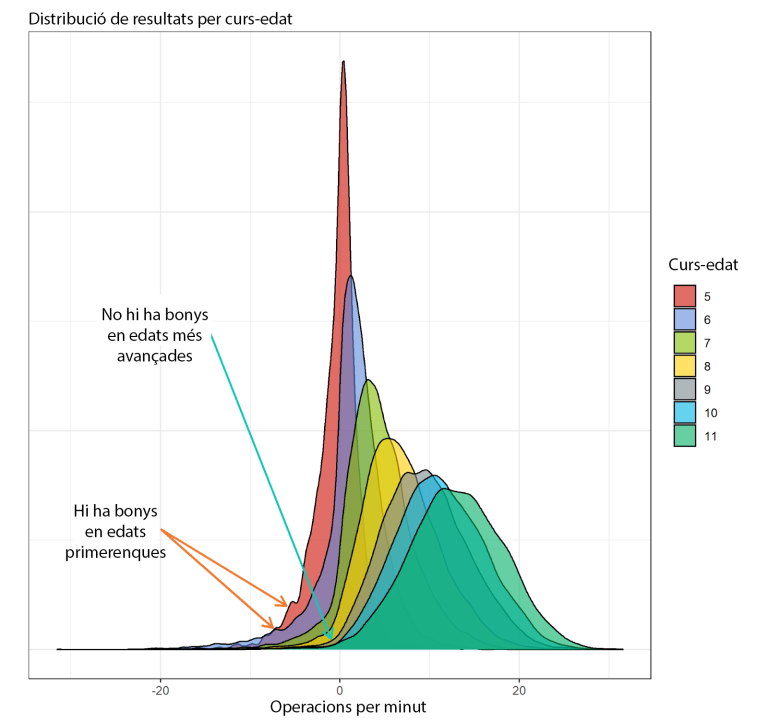
D’aquí, podem inferir dues coses: la primera és que hi ha infants que arriben a I5 o a 1r de primària amb un aprenentatge no formal de les matemàtiques molt deficient (habitualment proporcionat per la família, si no han estat escolaritzats) i, per tant, en veiem una quantitat més gran del que seria esperable en un percentil molt baix.
A mesura que aquest efecte és corregit per l’educació formal, el que veiem és que la distribució és cada vegada més normal (i. e., forma una campana de Gauss). D’això en podem inferir una conclusió molt rellevant: la discalcúlia (de la qual parlem en aquest altre article) no és un fenomen de «tot o res» (com tenir la grip o estar embarassada), sinó que és la cua d’una distribució normal (com la hipertensió o la hipercolesterolèmia). Aquest és un fet que es va descobrir fa 30 anys per a la dislèxia (Shaywitz, S. E. et al., 1992), però, pel que sabem, encara no s’ha demostrat per a la discalcúlia. Gràcies al present estudi i als que el seguiran, esperem poder-hi contribuir.
Shaywitz, S. E., Escobar, M. D., Shaywitz, B. A., Fletcher, J. M., & Makuch, R. (1992). Evidence that dyslexia may represent the lower tail of a normal distribution of reading ability. New England Journal of Medicine, 326(3), 145-150.






