Nella più che raccomandabile opera di Neus Sanmartí (2009) sulla valutazione, l’autore sostiene che alcuni degli aspetti da rivedere sono le attività proposte per valutare il livello di acquisizione delle competenze e che, se la valutazione continuerà a essere effettuata per mezzo delle tradizionali prove scritte con domande fondamentalmente riproduttive, non cambierà mai nulla.
A qualsiasi insegnante che abbia lavorato in una classe con bambini di 6 o 7 anni, questa riflessione risulterà ancora più familiare, poiché il grado di acquisizione della competenza linguistica a quell’età limita notevolmente la capacità di comunicare, argomentare o spiegare una strategia di risoluzione per iscritto. Quindi, al di là dei tradizionali test scritti, quali elementi possiamo considerare per valutare le competenze dei nostri alunni?
Valutare i processi con attività ricche
La chiave sta nel padroneggiare il quadro delle competenze (cioè sapere su quali processi stiamo lavorando e cosa ci aspettiamo dai nostri alunni) e osservare, ad esempio, le loro rappresentazioni visive o grafiche, o i loro interventi durante la conversazione in classe, soprattutto in età precoce.
In questo senso, abbiamo selezionato alcune attività ricche della proposta Innovamat, a nostro parere, particolarmente adatte alla valutazione delle competenze degli alunni relativamente allo sviluppo delle loro capacità matematiche. Non si tratta delle uniche attività adatte alla valutazione, ma forniscono senza dubbio consigli e indicazioni su come valutare qualsiasi altra attività ricca che noi insegnanti riteniamo opportuna.
Vediamo un esempio concreto, il caso reale di alcuni alunni di primo anno di scuola primaria che hanno svolto un’attività sulla misurazione. Nello specifico, abbiamo chiesto loro di misurare la lunghezza di alcuni oggetti rappresentati nel quaderno, utilizzando tre diverse unità di misura: dita, cubetti e una terza unità a loro scelta.
Cosa possiamo valutare in un’attività di questo tipo? Per cominciare, il conteggio risultativo da 1 a 20 e la scrittura dei numeri all’interno di questo intervallo. Si tratta di contenuti talmente necessari, la cui mancata padronanza può compromettere il corretto svolgimento dell’intera attività.
In questo caso, abbiamo osservato alcune risposte con numeri eccessivi, come «30 matite» o «54 dita». È possibile che il problema di un alunno che dà questo tipo di risposte abbia a che fare con il senso dei numeri più che con la misurazione.
Possiamo chiedere come si leggono questi numeri e se sono più grandi o più piccoli di altri numeri di riferimento.
Inoltre, è chiaro che gli alunni dovranno mettere in gioco alcune conoscenze specifiche sul significato di misura. Per verificare che lo facciano, potremmo chiederci:
- L’alunno utilizza una tecnica di misurazione accurata quando prende le misure con le dita?
In questo caso, l’alunno concatena gli indici di entrambe le mani, collocandoli in modo perpendicolare rispetto all’oggetto, il che gli permette di essere coerente e di ottenere sempre lo stesso risultato.
In questo caso, invece, l’alunno usa solo un dito indice per «saltare» sull’oggetto. Così facendo, perde il punto di riferimento esatto su cui era arrivato fino a quel momento e, riposizionando il dito, lascia degli spazi vuoti o torna a mettere il dito su uno spazio già misurato.
Possiamo fargli notare che questa tecnica non è molto accurata e può dare luogo a risultati sempre diversi, pur tornando a prendere le misure con lo stesso dito e usando la stessa tecnica.
Possiamo chiedergli: «Come puoi assicurarti di non tornare a mettere il dito su uno spazio che hai già misurato?».
Tra le diverse attività implicite in questo esercizio, la scelta oculata dell’unità di misura da utilizzare è sicuramente quella più basata sulle competenze. Potremmo chiederci:
- L'alunno si assicura di scegliere come unità di misura un oggetto che conservi sempre della stessa lunghezza?
In questo caso, l’alunno utilizza una gomma da cancellare senza cambiarne l’orientamento.
Qui, invece, prende le misure con le carte numeriche plastificate. In alcuni casi, misura partendo dal bordo plastificato trasparente, mentre in altri, misura partendo dalla parte bianca della carta, ignorando il bordo plastificato.
Possiamo fargli notare l’inadeguatezza del procedimento, chiedendogli di misurare nuovamente lo stesso oggetto e di verificare se ottiene lo stesso risultato.
Si tratta di un’attività che richiede l’applicazione di abilità proprie dei processi matematici. In termini di Risoluzione di problemi, potremmo chiederci:
- Quando diciamo all’alunno di scegliere un'unità di misura, trova la soluzione ottimale?
È interessante sottolineare che il concetto di «ottimale» può avere tante sfumature in funzione del criterio scelto dall’alunno. Qual era il suo obiettivo: la precisione o l’efficienza? O entrambe le cose?
Facciamo alcuni esempi diversi:
Questo alunno ha scelto una gomma da cancellare. In questo modo, è riuscito a essere preciso (riferendoci solo all’elemento e non alla tecnica, che influenzerà anche il grado di precisione), poiché applicando di volta in volta (dal punto iniziale a quello finale e poi dal precedente punto finale al nuovo punto finale e così via) questa unità di misura è possibile percorrere l’intera lunghezza dell’oggetto misurato. Inoltre, nel suo quaderno, ha scritto «4 e mezzo».
Questo alunno, invece, ha scelto una matita, il che gli ha permesso di essere ancora più efficiente: per dare la risposta gli è bastato appoggiare la matita sull’oggetto solo una volta.
In entrambi i casi sarebbe opportuno chiedere agli alunni quali criteri hanno utilizzato e quali altri potrebbero prendere in considerazione.
Anche in questo caso ci muoviamo all’interno del processo di Risoluzione di problemi. Potremmo chiederci:
- L’alunno verifica che la soluzione ottenuta sia ragionevole?
Senza valutare l’accuratezza delle misure adottate, possiamo soffermarci sulle risposte degli alunni e valutare se sono relazionate tra loro in modo ragionato.
Le risposte espresse in dita e cubetti sono coerenti con le illustrazioni: a colpo d’occhio, la lucertola è l’elemento più lungo e il millepiedi il più corto.
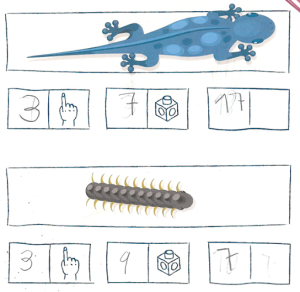
In questo caso, non è ragionevole che due illustrazioni che, a prima vista, hanno lunghezze chiaramente diverse diano le stesse misure (3 dita). La risposta diventa ancora meno coerente se le misurazioni eseguite con i cubetti danno risultati diversi.
In questo caso, potremmo porre domande e guidare l’alunno attraverso un ragionamento che gli permetta di considerare l’importanza di rivedere i risultati ottenuti.
Infine, potremmo porre alcune domande per fare una diagnosi del grado di acquisizione delle capacità relative al processo di Ragionamento e prova:
- L’alunno è in grado di giustificare il motivo per cui prende le misure in un determinato modo?
Questo alunno usa tutte e 5 le dita contemporaneamente per prendere le misure. Possiamo chiedergli perché lo fa.
Potrebbe non sapersi giustificare o, al contrario, potrebbe spiegare che in questo modo prende le misure più velocemente. E un’ultima domanda legata al processo di Ragionamento e prova:
- L'alunno nota che eseguire misurazioni con i cubetti è più affidabile rispetto a farlo con le dita?
Come abbiamo detto all’inizio, chiedere a un alunno di 6 o 7 anni di mettere per iscritto un ragionamento può non essere il modo migliore per valutare lo sviluppo delle sue capacità relative ai processi matematici. Per questo motivo, bisogna prendere in considerazione anche la possibilità di valutare le conversazioni che hanno luogo in classe:
Lo svolgimento della conversazione in classe permette all’insegnante di gestirla al momento e di interpretare più chiaramente il reale ragionamento dell’alunno nel caso in cui, ad esempio, risponda in modo vago.
La valutazione con Innovamat
Noi di Innovamat riteniamo che l’attività di valutazione abbia principalmente una funzione formativa; in altre parole, deve permettere agli alunni di regolare il proprio processo di apprendimento. Condividere con gli alunni i nostri ragionamenti su situazioni e casi come quelli dettagliati in questo articolo, li aiuterà sicuramente nella scelta di strategie efficienti che permettano loro di trovare i risultati ottimali. Aiutandoli, avremo già eseguito la nostra valutazione, e non dato un giudizio.
Se vogliamo usare questa attività per dare un giudizio sui risultati del processo di apprendimento (dare dei voti), potremmo usare le domande che abbiamo esaminato in questo articolo come indicatori di valutazione e, se lo riteniamo opportuno, attribuirgli un valore numerico o di giudizio.
Come abbiamo visto, sapere cosa possiamo osservare in ogni momento e avere a disposizione alcuni esempi di risposte reali degli alunni ci aiuta a portare a termine la difficile attività di valutazione.
- NCTM (2000): Principles and Standards for School Mathematics. Reston, VA, Stati Uniti
- Sanmartí, N. (2020) Avaluar és aprendre: L’avaluació per millorar els aprenentatges de l’alumnat en el marc del currículum per competències.
- Direcció General de Currículum i Personalització. Dipartimento di Educazione. Barcellona, Spagna
